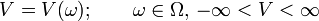Proceso estocástico

Proceso estocástico

Saltar a navegación, búsqueda

El índice de la bolsa es un ejemplo de proceso estocástico de tipo no estacionario (por eso no se puede predecir)

En estadística, y en concreto teoría de la probabilidad, un proceso aleatorio o proceso estocástico es un concepto matemático que sirve para caracterizar es una sucesión de variables aleatorias (estocásticas) que evolucionan en función de otra variable, generalmente, el tiempo. Cada una de las variables aleatorias del proceso tiene su propia función de distribución de probabilidad y, entre ellas, pueden estar correlacionadas o no.

Cada variable o conjunto de variables sometidas a influencias o impactos aleatorios constituye un proceso estocástico.

Ejemplos

• Los siguientes son ejemplos dentro del amplio grupo de las series temporales:
  • Señales de telecomunicación
  • Señales biomédicas (electrocardiograma, encefalograma, etc.)
  • Señales sísmicas
  • El número de manchas solares año tras año
  • El índice de la bolsa segundo a segundo
  • La evolución de la población de un municipio año tras año
  • El tiempo de espera en cola de cada uno de los usuarios que van llegando a una ventanilla
  • El clima es un gigantesco cúmulo de procesos estocásticos interrelacionados (velocidad del viento, humedad del aire, etc) que evolucionan en el espacio y en el tiempo.
  • Los procesos estocásticos de orden mayor a uno, como el caso de una serie de tiempo de orden 2 y una correlación de cero con las demás observaciones.

Definición matemática

Un proceso estocástico se puede definir equivalentemente de dos formas diferentes:

• Como un conjunto de realizaciones temporales y un índice aleatorio que selecciona una de ellas.
• Como un conjunto de variables aleatorias 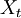$X_t\,$ indexadas por un índice 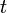$t\,$, dado que 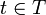$t \in T\,$, con $T\subseteq\mathbb{R}\,$.

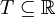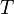$T\,$ puede ser continuo si es un intervalo (el número de sus valores es ilimitado) o discreto si es numerable (solamente puede asumir determinados valores).

Las variables aleatorias 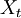$X_t\,$ toman valores en un conjunto que se denomina espacio probabilístico.

Sea 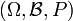$(\Omega , \mathcal B , P )$ un espacio probabilístico.

En una muestra de tamaño n se observa un suceso compuesto E formado por sucesos elementales ω:

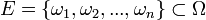$E = \{\omega_1, \omega_2, ..., \omega_n\} \sub \Omega\,$, de manera que $E \isin B\,$.

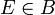El suceso compuesto es un subconjunto contenido en el espacio muestral y es un álgebra de Boole B. A cada suceso ω le corresponde un valor de una variable aleatoria V, de manera que V es función de ω:

$V = V(\omega); \qquad \omega\in\Omega,\, -\infty < V < \infty$

El dominio de esta función o sea el campo de variabilidad del suceso elemental, es el espacio muestral, y su recorrido, o sea el de la variable aleatoria, es el campo de los números reales. Se llama proceso aleatorio al valor en 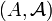$(A, \mathcal A)$ de un elemento 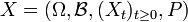$X = (\Omega,\mathcal B,(X_t)_{t\ge 0},P)$, donde para todo 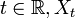$t\in \mathbb{R}, X_t\,$ es una variable aleatoria del valor en $(A,\mathcal A)$.

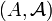Si se observa el suceso ω en un momento t de tiempo:

$V = V(\omega, t), \qquad \omega\in\Omega, t\in T, -\infty < V < \infty$.

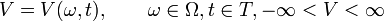V define así un proceso estocástico.^[1]

Si 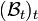$({\mathcal B}_t)_t\,$ es una filtración,^[2] se llama proceso aleatorio adaptado, al valor en 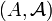$(A,\mathcal A)$, de un elemento 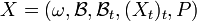$X=(\omega,\mathcal B,\mathcal{B}_t,(X_t)_t,P)$, donde 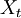$X_t\,$ es una variable aleatoria 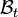$\mathcal{B}_t$ -medible del valor en 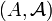$(A,\mathcal A)$. La función 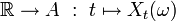$\mathbb R \rightarrow A\ : \ t \mapsto X_t(\omega)$ se llama la trayectoria asociada al suceso $\omega \,$.

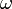Casos especiales

• Proceso estacionario: Un proceso es estacionario en sentido estricto si la función de distribución conjunta de cualquier subconjunto de variables es constante respecto a un desplazamiento en el tiempo. Se dice que un proceso es estacionario en sentido amplio (o débilmente estacionario) cuando se verifica que:

1. La media teórica es independiente del tiempo; y
2. Las autocovarianzas de orden s sólo vienen afectadas por el lapso de tiempo transcurrido entre los dos periodos y no dependen del tiempo.

• Proceso homogéneo: variables aleatorias independientes e idénticamente distribuidas
• Proceso de Márkov: Aquellos procesos discretos en que la evolución sólo depende del estado actual y no de los anteriores.
• Proceso de Gauss: Proceso continuo en el que toda combinación lineal de variables es una variable de distribución normal.
• Proceso de Poisson
• Proceso de Gauss-Márkov: Son procesos, al mismo tiempo, de Gauss y de Márkov
• Proceso de Bernoulli Son procesos discretos con una distribución binomial.

Referencias

1. ↑ Dagum, Camilo y Estela M. Bee de Dagum(1971) Introducción a la Econometría: 79-83. México: Siglo XXI editores, sétima edición, 1980.
2. ↑ Se llama "filtración" a una sucesión {B (t), t ∈T}de sub-σ-álgebras tal que B (t) está incluida en B (r) si r <t.

Obtenido de "Proceso estoc%C3%A1stico"