- Proyección ortogonal
-
Proyección ortogonal
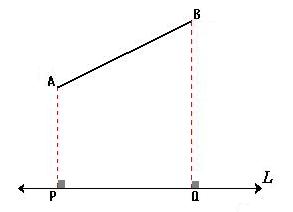
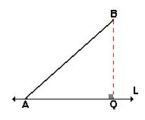
La proyección ortogonal del segmento AB sobre la recta L es el segmento PQ.En la geometría Euclidiana, Proyección ortogonal es aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección, estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.
En el plano, la proyección ortogonal es aquella cuyas líneas proyectantes auxiliares son perpendiculares a la recta de proyección L.
Así, dado un segmento AB, bastará proyectar los puntos "extremos" del segmento –mediante líneas proyectantes auxiliares perpendiculares a L–, para determinar la proyección sobre la recta L.
Una aplicación de proyecciones ortogonales son los teoremas de las Relaciones métricas en el triángulo mediante las cuales se puede calcular la dimensión de los lados de un triangulo.
El concepto de proyección ortogonal se generaliza a espacios euclidianos de dimensión arbitraria, inclusive de dimensión infinita. Esta generalización juega un papel importante en muchas ramas de matemática y física.
Casos de proyección ortogonal en el plano
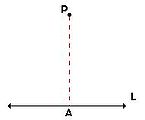
Proyección ortogonal de un punto:
- La proyección ortogonal de un punto P es otro punto A, situado sobre L, que se obtiene trazando una línea perpendicular a L desde el punto A.
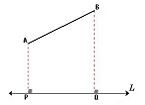
Proyección ortogonal de un segmento:
- Caso general: si el segmento dado AB no es paralelo la recta L, la proyección ortogonal es segmento PQ que se obtiene trazando líneas perpendiculares a L desde los puntos extremos. La magnitud de la proyección siempre es menor que la del segmento dado.
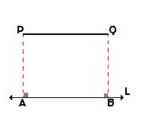
- Si el segmento PQ y la recta L son paralelos, la proyección será: AB = PQ, que se obtiene de forma análoga.
- Si el segmento AB tiene un punto común con la recta L, la proyección se obtiene de modo similar.
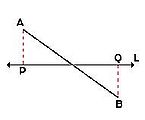
- Si el segmento AB corta a la recta L, la proyección se obtiene de forma análoga.
Véase también
Categoría: Geometría
Wikimedia foundation. 2010.