- Racionalización de radicales
-
Racionalización de radicales
La racionalización de radicales es un proceso donde se tiene que eliminar el radical o los radicales, que están en el denominador de la fracción.
Racionalizar una fracción con raíces en el denominador, es encontrar otra expresión equivalente que no tenga raíces en el denominador. Para ello se multiplica el numerador y el denominador por la expresión adecuada, de forma que al operar desaparezca la raíz del denominador.Contenido
Racionalización de un monomio de índice 2
Para racionalizar un monomio de este tipo se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma.
Ejemplo:
En este caso hay que multiplicar numerador y denominador por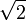
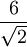 ·
· 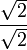 =
= 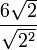
Después se despeja la raíz cuadrada del denominador ya que la cantidad subradical que es 2 elevada al cuadrado puede eliminar o despejar la raíz cuadrada: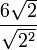 =
= 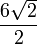
El resultado del ejercicio es éste, aunque se puede simplificar el número entero del numerador entre el del denominador, así: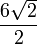 =
= 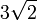
Racionalización de binomio de índice 2
Para racionalizar un binomio de índice 2, se debe hacer un proceso similar al ejercicio anterior, multiplicar el numerador y denominador de la fracción por el denominador de la misma.
Ejemplo:
En este caso hay que multiplicar el numerador y el denominador por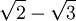 ; este resultado es el que da el producto notable de los binomios conjugados.
; este resultado es el que da el producto notable de los binomios conjugados.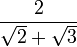 ·
· 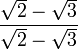 =
= 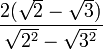
Ahora, se procede al despeje de las raíces cuadradas del denominador: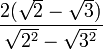 =
= 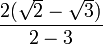 =
= 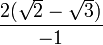 =
= 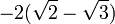
Racionalización de monomios con índices mayores que 2
Ejemplo:
Primero, todas las cantidades subradicales (si son números enteros elevados que no tienen exponente) se les debe obtener la raíz enésima.![\frac{{2}}{\sqrt[5]{8a^3b^4}}](/pictures/eswiki/50/28b560d173a879a45f5a697d212ec501.png) =
= ![\frac{{2}}{\sqrt[5]{2^3a^3b^4}}](/pictures/eswiki/56/81a07829eb2a526acc5c99c442f8095e.png)
Ahora, la cantidad que deberá ser multiplicada al numerador y denominador de la fracción sigue un procedimiento diferente a las anteriores.
Las cantidades exponenciales de los subradicales del radical para multiplicar al numerador y denominador de la fracción será el número del exponente que falta para acercarse al índice del radical. En caso de que el exponente sea mayor que el índice de la raíz, la cantidad de aquel exponente será la que falte para llegar al múltiplo más cercano de la raíz.![\sqrt[5]{2^3a^3b^4}](/pictures/eswiki/54/61a85ad591337a262827c9f70a243502.png) =
= ![\sqrt[5]{2^2a^2b}](/pictures/eswiki/100/df02d0fc08b6bcf7796710b87403d98a.png)
En este ejemplo, es![\sqrt[5] {2^2a^2b}](/pictures/eswiki/100/df02d0fc08b6bcf7796710b87403d98a.png) , ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz.
, ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz.Ahora, se procede a multiplicar el numerador y el denominador:
![\frac{{2}}{\sqrt[5]{2^3a^3b^4}}](/pictures/eswiki/56/81a07829eb2a526acc5c99c442f8095e.png) ·
· ![\frac{\sqrt[5] {2^2a^2b} }{\sqrt[5]{2^2a^2b}}](/pictures/eswiki/56/89315c6b50c3027d25e1f1e95b61d6fd.png) =
= ![\frac{{2\sqrt[5]{2^2a^2b}}}{\sqrt[5]{2^5a^5b^5}}](/pictures/eswiki/101/e393322e7e2301bdd0c26b9df0405992.png)
Ahora, se procede al despeje de las raíces, en el ejemplo de índice 5:
![\frac{{2\sqrt[5]{2^2a^2b}}}{\sqrt[5]{2^5a^5b^5}}](/pictures/eswiki/101/e393322e7e2301bdd0c26b9df0405992.png) =
= ![\frac{{2\sqrt[5]{4a^2b}}}{{2ab}}](/pictures/eswiki/49/157186c3d733b0a6317bfe11b3bbd31a.png)
Ahora, se procede a la simplificación, que sería el último paso de la operación:
![\frac{{2\sqrt[5]{4a^2b}}}{{2ab}}](/pictures/eswiki/49/157186c3d733b0a6317bfe11b3bbd31a.png) =
= ![\frac{{\sqrt[5]{4a^2b}}}{{ab}}](/pictures/eswiki/97/aa4f5f2ff57625eeecb4f8ca585d8d45.png)
Racionalización de binomios con índices mayores que 2
Cuando se tienen binomios con radical de índice 3, es preciso utilizar productos notables, en este caso la adición y sustracción de cubos, según sea el caso.
Adición de cubos: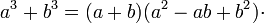
Sustracción de cubos: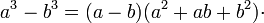
Ejemplo:
Se multiplica el numerador y el denominador de la fracción por el resultado que dé el producto notable del denominador.![\sqrt[3]{a}-\sqrt[3]{b}](/pictures/eswiki/49/1142fc632406f730c6d150aba9b08a5e.png) =
= ![(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2](/pictures/eswiki/99/caf7cb9108314ed9a5b309cb1235dcfb.png) ... para este caso se aplica sustración de cubos como se muestra arriba.
... para este caso se aplica sustración de cubos como se muestra arriba.
Este es el resultado del producto notable, que irá en el denominador, que multiplicará tanto al numerador como al denominador:![\frac{{1}}{\sqrt[3]{a}-\sqrt[3]{b}}](/pictures/eswiki/98/b4bb468eebe86398e4e66a6e93c2d59b.png) ·
· ![\frac{(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2}{(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2}](/pictures/eswiki/102/f3d325f5dce87a6e21a2af8027a5debe.png) =
= ![\frac{{(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2}}{{\sqrt[3]{a}-\sqrt[3]{b}}[(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2]}](/pictures/eswiki/51/32167c56f8a46e43d17e8478fa3c0324.png)
Ahora, se resuelven las potencias que están fuera del paréntesis:
![\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{\sqrt[3]{a}-\sqrt[3]{b}}[(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2]}](/pictures/eswiki/48/0fac0bbf902061f2a0eab6ab1e47b660.png)
Ahora, el denominador se transforma el resultado a producto notable:![\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{\sqrt[3]{a}-\sqrt[3]{b}}[(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2]}](/pictures/eswiki/48/0fac0bbf902061f2a0eab6ab1e47b660.png) =
= ![\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{\sqrt[3]{a^3}-\sqrt[3]{b^3}}}](/pictures/eswiki/50/2735ea6cececc99667244842eee920c8.png)
Ya que los exponentes de las cantidades subradicales del denominador son iguales o múltiplos de 3, puede procederse al despeje del radical del denominador, que es el último paso de la racionalización:
![\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{\sqrt[3]{a^3}-\sqrt[3]{b^3}}}](/pictures/eswiki/50/2735ea6cececc99667244842eee920c8.png) =
= ![\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{{a}-{b}}}](/pictures/eswiki/48/0443828f1f2149056f91096297979fe4.png)
Véase también
Bibliografía
Suárez Bracho, Estrella y Durán Cepeda, Darío (2003) Matemáticas Noveno año. Caracas: Editorial Santillana.
Categorías: Álgebra elemental | Raíces
Wikimedia foundation. 2010.
