Radio de curvatura

Radio de curvatura

Saltar a navegación, búsqueda

El radio de curvatura es una magnitud que mide la curvatura de un objeto geométrico tal como una línea curva, una superficie o más en general una variedad diferenciable embebida en un espacio euclídeo.

Líneas Curvas

El radio de curvatura de una línea curva o un objeto aproximable mediante una curva es una magnitud geométrica que puede definirse en cada punto de la misma que coincide con el inverso de la curvatura en cada punto:

$R_c(s) := \frac{1}{\chi(s)}$

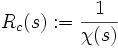
Por otro lado la curvatura es una medida del cambio que sufre la dirección del vector tangente a una curva cuando nos movemos a lo largo de ésta. Para una curva parametrizada cualquiera la curvatura y el radio de curvatura vienen dados por:

$\frac{1}{R_c(t)} = \chi(t) = \frac {\left\vert \dot\mathbf{r}(t) \times \ddot\mathbf{r}(t) \right\vert } {\left\vert \dot\mathbf{r}(t) \right\vert ^3}$

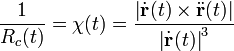
Si en lugar de un parámetro cualquiera usamos el parámetro de longitud de arco, la anterior ecuación se simplica mucho, por resultar un vector tangente constante, y puede escribirse como:

$\frac{1}{R_c(s)}= \chi(s) = \left\vert \mathbf{\tilde{r}}''(s) \right\vert$

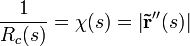
Curvas planas

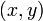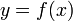Para una curva plana cuya ecuación pueda escribirse en coordenadas cartesianas $(x, y)\,$ como $y = f(x)\,$ el radio de curvatura se puede calcular simplemente como:

$R_c = \frac{\left[ 1+ \left(\frac{df}{dx}\right)^2\right]^{\frac{3}{2}}}{\left | \frac{d^2f}{dx^2}\right \vert}$

Superficies

Artículo principal: geometría diferencial de superficies

Una superficie embebida en el espacio euclídeo tridimensional se caracteriza en cada uno de sus puntos por dos radios de curvatura. El centro de ambos radios de curvatura está situado sobre la recta que contiene al vector normal a la superficie. Si los dos radios de curvatura son finitos entonces se tiene:

• En un punto elíptico de una superficie, los dos centros de curvatura están situados del mismo lado de la superficie, la curvatura gaussiana es positiva.
• En un punto hiberbólico de una superficie, los dos centros de curvatura están situados en diferentes lados de la superficie, la curvatura gaussiana es negativa.
• En un punto parabólico de una superficie, uno de los radios de curvatura es inifinito.

Obtenido de "Radio de curvatura"