- Radio hidráulico
-
Radio hidráulico
El radio hidráulico, es un parámetro importante en el dimensionado de canales, tubos y otros componentes de las obras hidráulicas, generalmente es representado por la letra R, y expresado en m es la relación entre:
- El área mojada (A, en m²).
- El perímetro mojado (P, en m).
Es decir:
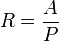
Las expresiones que permiten su cálculo son función de la forma geométrica de la sección transversal del canal.
Contenido
Canales de sección rectangular
Donde: L = ancho de la base del canal (en m).
- Área mojada:
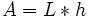
- Perímetro mojado:
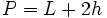
Muy importante, tomaremos el valor de nuestra " h " hasta donde llegue el nivel del agua dentro de la sección rectangular.Es decir, si llena toda la altura de nuestra sección, tomaremos la altura de este canal. En cambio, si el nivel de agua solo llega hasta la mitad de este, tomaremos h/2.
Y así actuaremos con cualquier nivel de agua dentro de nuestro canal.
Por eso el nombre de área mojada y perímetro mojado.
Canales de sección triangular
Donde:
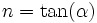 siendo: (α) el ángulo del talud con la vertical.
siendo: (α) el ángulo del talud con la vertical.- Área mojada:
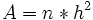
- Perímetro mojado:
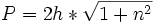
Canales de sección trapezoidal
- Área mojada:
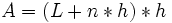
- Perímetro mojado:
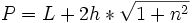
Canales de sección circular
Donde: r = radio de la sección circular (en m); la sección mojada limitada por la cuerda c, que sostiene el ángulo al centro Φ medido en grados sexagesimales. [α cuando se expresa en radianes]
- Área mojada:
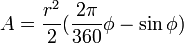 ; o expresando el ángulo en radianes :
; o expresando el ángulo en radianes : 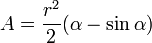
- Perímetro mojado:
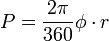 ; o igualmente
; o igualmente 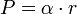
- Y por tanto Radio hidraulico:
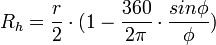 ; o igualmente
; o igualmente 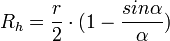
El calado que proporciona el radio hidráulico máximo (lo que significa caudal máximo a igualdad de otras variables) corresponde al valor de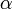 que hace mínima la expresión
que hace mínima la expresión 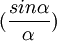 . Esta ecuación es una ecuación trascendente, con varios mínimos, que se pueden obtener resolviendo otra ecuación trascendente, la
. Esta ecuación es una ecuación trascendente, con varios mínimos, que se pueden obtener resolviendo otra ecuación trascendente, la 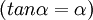 . La primera solución de esta ecuación (que es la que vale para obtener el ángulo y el calado buscados), obtenida por métodos numéricos, es
. La primera solución de esta ecuación (que es la que vale para obtener el ángulo y el calado buscados), obtenida por métodos numéricos, es 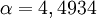 rad, y
rad, y 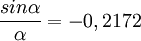 . Por tanto,
. Por tanto,El Radio hidraulico máximo de una conducción circular es :
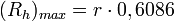
En el caso particular de las conducciones circulares trabajando con sección plena, es decir en presión, el radio hidráulico en función del diámetro
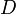 es:
es: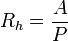
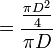 ; es decir :
; es decir : 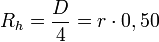
De lo anterior se deduce que el radio hidráulico a sección llena es el 82,2% del radio hidráulico máximo que puede proporcionar la sección circular. En la fórmula del caudal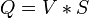 el valor del radio hidráulico interviene con un exponente de 2/3 (del término de velocidad de la Fórmula de Manning), pero interviene también la sección mojada, que depende del ángulo
el valor del radio hidráulico interviene con un exponente de 2/3 (del término de velocidad de la Fórmula de Manning), pero interviene también la sección mojada, que depende del ángulo 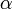 , con lo que el caudal que una sección circular es capaz de transportar a sección llena es aproximadamente el 93% del máximo. Este valor máximo, que es un 7,5 % mayor que el de la sección llena, se consigue cuando queda una pequeña sección superior libre (correspondiente a
, con lo que el caudal que una sección circular es capaz de transportar a sección llena es aproximadamente el 93% del máximo. Este valor máximo, que es un 7,5 % mayor que el de la sección llena, se consigue cuando queda una pequeña sección superior libre (correspondiente a 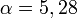 rad aproximadamente).
rad aproximadamente).Canales de secciones especiales
Se han usado en el pasado y se siguen usando, especialmente para canalizaciones de aguas servidas, o canalizaciones mixtas de aguas servidas y aguas de lluvia, donde la variación de caudales en el tiempo puede ser considerable, secciones especiales o compuestas. En estos casos la determinación de los parámetros A, P y R se realiza caso por caso en función de la geometría de la sección. El radio hidráulico de un canal o ducto, generalmentre representado por la letra R y expresado en m, es la relación entre:
- El área mojada (A, en m²); y,
- El perímetro mojado (P, en m)
Su determinación es función de la forma geométrica del canal.
Canales de sección irregular
Es el caso general para los canales naturales, pero existen también canales construidos con secciones geométricas definidas, y que en el transcurso del tiempo, por efecto de la erosión, se han transformado en irregulares y deben ser tratados como tales para obtener resultados de análisis correctos.
En estos casos se determina, durante visitas de campo, los tramos que se pueden considerar homogéneos con buena aproximación. Después del levantamiento topográfico y batimétrico de la sección, se divide la misma en fajas verticales. Para cada faja vertical "i" se determina Ai, considerándolo un triángulo, o un trapecio; y como Pi, se considera el respectivo tramo de fondo. De esta forma el cálculo del área mojada y del perímetro mojado se hace con las expresiones:
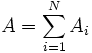
y
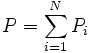
Usos del radio hidráulico
El radio hidáulico se emplea en el cálculo de pérdidas de carga según, la fórmula de Manning:
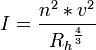
donde: I es el gradiente hidráulico, o perdida de carga por unidad de longitud; n es el coeficiente de Manning, v la velocidad del fluido y Rh el radio hidráulico. Evidentemente las unidades deben ser coherentes entre si.
Referencias
- Hidráulica de los canales abiertos. Ven Te Chow. 1982. ISBN 968-13-1327-5
- Conocimientos impartidos en Universidad Politécnica de Cartagena, Máquinas Hidráulicas.
Categoría: Hidráulica
Wikimedia foundation. 2010.
