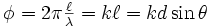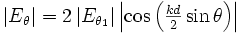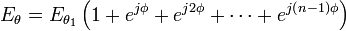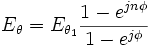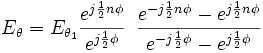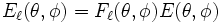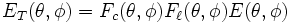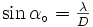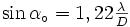- Red de antenas
-
Red de antenas
Una red de antenas es un conjunto de antenas iguales, separadas, con la misma orientación y alimentadas sincrónicamente. Es decir que el desfase de la corriente entre cada par de antenas es constante. Una red de antenas puede incluir elementos que no están alimentados directamente, sino que están alimentados por la radiaciones de otros elementos (es el caso de las antenas Yagi-Uda). El campo eléctrico y magnético producido por una red de antenas es la suma vectorial de los campos producidos por cada una de las antenas. Además de la dirección y de la amplitud de los campos, cuando se calcula la suma, hay que tener en cuenta la fase de cada uno de los campos. Esa fase depende de la fase de la corriente en cada una de las antenas y de la distancia al punto donde se hace la suma, que suele ser diferente para cada uno de los elementos y que añade o disminuye el desfase.
Contenido
Radiación de un par de antenas
 Las ondas que salen de 2 llegan al punto de observación en avance de fase.
Las ondas que salen de 2 llegan al punto de observación en avance de fase.Sean dos antenas idénticas separadas de una distancia
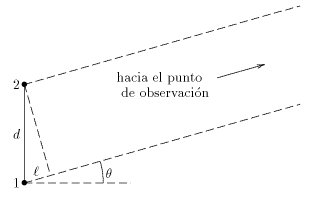
 y alimentadas en fase (es decir, desfase cero). Calculemos el campo eléctrico producido por ese par de antenas a gran distancia de las antenas, es decir que
y alimentadas en fase (es decir, desfase cero). Calculemos el campo eléctrico producido por ese par de antenas a gran distancia de las antenas, es decir que  es muy grande comparado a la longitud de onda
es muy grande comparado a la longitud de onda 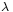 y que
y que 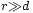 Como la distancia
Como la distancia  es grande, el angulo
es grande, el angulo  es el mismo para las dos antenas y el campo producido por cada una será el mismo:
es el mismo para las dos antenas y el campo producido por cada una será el mismo: 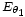 y
y 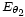 . Pero si la amplitud es la misma, la fase no lo será ya que la antena 2 está más cerca del punto donde calculamos. El campo producido por la antena 2 llegará
. Pero si la amplitud es la misma, la fase no lo será ya que la antena 2 está más cerca del punto donde calculamos. El campo producido por la antena 2 llegará 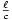 segundos antes que el campo producido por la antena 1. Quiere decir que el campo de la antena 1 estará en avance de fase
segundos antes que el campo producido por la antena 1. Quiere decir que el campo de la antena 1 estará en avance de faseAquí,
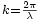 es el número de onda.
es el número de onda.Como los dos campos son paralelos, la suma vectorial se reduce a sumar las amplitudes, pero teniendo en cuenta del desfase:
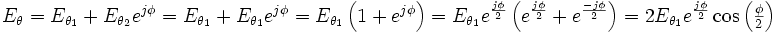
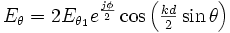
Como la fase del campo eléctrico recibido no presenta ningún interés y que únicamente la amplitud es importante, solo al módulo de este número complejo nos interesa:
Es fácil ver que para
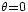 el campo eléctrico es máximo y que es igual al doble del campo producido por cada una de las antenas. Es lógico ya que para
el campo eléctrico es máximo y que es igual al doble del campo producido por cada una de las antenas. Es lógico ya que para 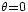 las dos emisiones han recorrido la misma distancia y llegan en fase. En cambio, el campo emitido sera cero cuando el coseno valga cero. Eso sucede la primera vez cuando
las dos emisiones han recorrido la misma distancia y llegan en fase. En cambio, el campo emitido sera cero cuando el coseno valga cero. Eso sucede la primera vez cuando 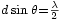 . Es decir, cuando la diferencia de distancia recorrida es igual a media longitud de onda y que las dos emisiones llegan desfasadas de 180°. Para
. Es decir, cuando la diferencia de distancia recorrida es igual a media longitud de onda y que las dos emisiones llegan desfasadas de 180°. Para  más grande, la diferencia de fases va hacia 360° y, para ese valor, la emisión será de nuevo máxima. Cada vez que
más grande, la diferencia de fases va hacia 360° y, para ese valor, la emisión será de nuevo máxima. Cada vez que 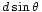 es igual a un múltiplo impar de
es igual a un múltiplo impar de 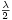 la emisión pasa por cero y cada vez que
la emisión pasa por cero y cada vez que 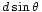 es igual a un múltiplo par de
es igual a un múltiplo par de 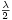 la emisión es máxima. Pero no hay que olvidar que
la emisión es máxima. Pero no hay que olvidar que  no puede aumentar indefinidamente ya que su valor esta comprendido entre -90° y +90°.
no puede aumentar indefinidamente ya que su valor esta comprendido entre -90° y +90°.Tampoco hay que olvidar que la emisión es simétrica alrededor del eje que pasa por las dos antenas.
Las antenas tienen un diagrama de emisión propio. El campo que hemos calculado solo tiene en cuenta el aspecto interferencia entre las dos ondas emitidas por cada una de las antenas. En el calculo y la visualización del resultado, hay que tener también en cuenta el diagrama de radiación de las antenas. Por ejemplo, el cálculo que hemos hecho puede dar un máximo hacia
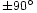 . Pero si las antenas son dipolos alineados con el eje que las contiene, el resultado no será un máximo sino un cero, ya que los dipolos no emiten en esa dirección.
. Pero si las antenas son dipolos alineados con el eje que las contiene, el resultado no será un máximo sino un cero, ya que los dipolos no emiten en esa dirección.He aquí un ejemplo formado por dos antenas dipolos verticales
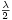 separadas de una distancia
separadas de una distancia 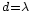
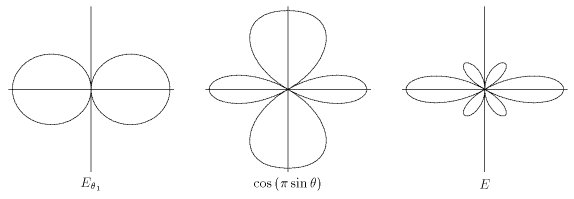 Para obtener el diagrama de radiación final hay que multiplicar el diagrama debido a la interferencia con el diagrama de los radiadores individuales.
Para obtener el diagrama de radiación final hay que multiplicar el diagrama debido a la interferencia con el diagrama de los radiadores individuales.A la izquierda hemos dibujado el diagrama de radiación de un dipolo
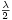 . En el centro, el diagrama de radiación debido a las interferencias entre las dos antenas. El diagrama de radiación resultante se encuentra a la derecha y es el resultado de multiplicar los dos diagramas. Los tres dibujos son simétricos alrededor del eje vertical.
. En el centro, el diagrama de radiación debido a las interferencias entre las dos antenas. El diagrama de radiación resultante se encuentra a la derecha y es el resultado de multiplicar los dos diagramas. Los tres dibujos son simétricos alrededor del eje vertical.
Red de antenas a emisión transversal
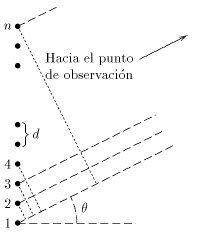 Las ondas emitidas por los radiadores de arriba llegan con avance de fase con respecto a los radiadores de abajo.
Las ondas emitidas por los radiadores de arriba llegan con avance de fase con respecto a los radiadores de abajo.Sean n radiadores alineados, alimentados en fase y a una distancia
 entre cada uno. Examinemos el campo lejano
entre cada uno. Examinemos el campo lejano 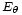 radiado en la dirección
radiado en la dirección  . Si tomamos como referencia de fase la del campo lejano
. Si tomamos como referencia de fase la del campo lejano 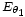 radiado por el radiador número 1, el campo del radiador número 2 tendrá un avance de fase de
radiado por el radiador número 1, el campo del radiador número 2 tendrá un avance de fase de 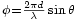 . El del radiador número 3 tendrá un avance de fase de
. El del radiador número 3 tendrá un avance de fase de 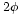 y lo mismo con los siguientes. Para calcular el campo total, basta sumar todos los campos teniendo en cuenta el desfase. Como todas las amplitudes son iguales:
y lo mismo con los siguientes. Para calcular el campo total, basta sumar todos los campos teniendo en cuenta el desfase. Como todas las amplitudes son iguales:como conocemos la suma de una serie geométrica:
Como solo nos interesa la amplitud, la primera fracción desaparece y, utilizando la fórmula de Euler, podemos escribir:
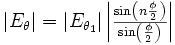 .
.
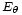 presenta máximos y ceros en función de
presenta máximos y ceros en función de 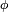 , o sea en función de
, o sea en función de  . Pero esos máximos no tienen todos el mismo valor. El primero vale
. Pero esos máximos no tienen todos el mismo valor. El primero vale 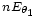 y los siguientes son más pequeños y sus valores dependen de
y los siguientes son más pequeños y sus valores dependen de 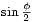 . El primer cero ocurre cuando
. El primer cero ocurre cuando 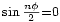 . O sea cuando
. O sea cuando 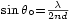 . Como
. Como 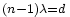 encontramos una relación similar a la que habíamos calculado para dos antenas: el primer cero aparece cuando los desfases de cada una de las antenas están distribuidos uniformemente entre 0° y 360° (0 y
encontramos una relación similar a la que habíamos calculado para dos antenas: el primer cero aparece cuando los desfases de cada una de las antenas están distribuidos uniformemente entre 0° y 360° (0 y 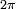 radianes en medidas científicas). El cero siguiente aparece cuando los desfases están distribuidos uniformemente entre 0° y 720° (0 y
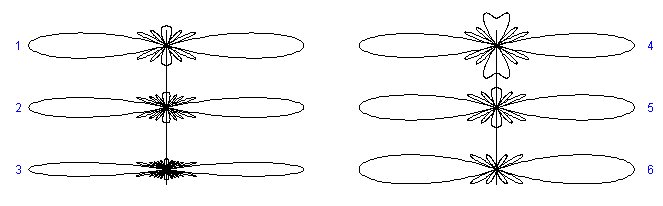
radianes en medidas científicas). El cero siguiente aparece cuando los desfases están distribuidos uniformemente entre 0° y 720° (0 y 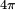 radianes), etc.
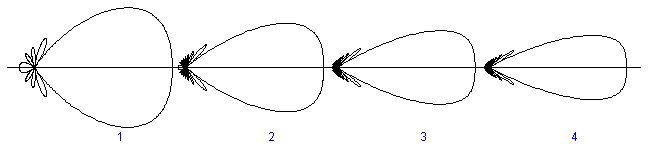
radianes), etc.En la figura siguiente hemos trazado los diagramas de radiación de algunos casos particulares. Solo el aspecto interferencia entre antenas esta dibujado. Para obtener el diagrama verdadero habría que multiplicar esos diagramas por el diagrama de emisión de las antenas individuales. En el dibujo las redes de antenas son verticales.
Diagramas de radiación de una red de antenas isótropas a emisión transversal Número del diagrama Número de antenas separación entre antenas Longitud total 1 7 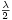
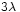
2 9 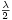
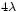
3 17 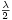
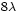
4 5 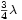
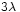
5 7 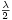
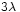
6 infinito 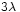
Los diagramas de la izquierda muestran la influencia de la longitud total de la red. A medida que la longitud total aumenta, el lóbulo principal se hace más estrecho y los lóbulos segundarios se hacen más numerosos y más pequeños. Los diagramas de derecha muestran la influencia de aumentar el número de antenas conservando la misma longitud total. Cuando el número aumenta, la amplitud de los lóbulos segundarios disminuye, pero tienden hacia un valor diferente de cero.
Red de antenas a emisión longitudinal
En la red de antenas a emisión transversal el lóbulo máximo de emisión se sitúa en un plan "ecuatorial" porque, en ese plano, y lejos de la red, todo punto está situado a la misma distancia de cada una de las antenas.
Imaginemos que esta vez alimentamos cada antena con un retardo de fase con respecto a su vecina inferior. En ese caso, para recibir todas las emisiones al mismo tiempo (en fase), en lugar que ponerse en el plano ecuatorial, habrá que ponerse un poco más arriba. El plano del lóbulo máximo se ha transformado en la superficie de un cono (cuyo ápice está en la red). Si aumentamos aun el retardo de fase, el cono se cerrará más aún y llegará el momento en el cual el cono estará cerrado completamente y se habrá transformado en una recta alineada con las antenas. Para llegar a esa situación hace falta que el retardo de fase de cada antena corresponda al tiempo necesario para que la emisión de su vecina de abajo llegue a ella. Si la distancia entre las antenas es
 , el retardo de fase será
, el retardo de fase será 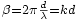 . La fórmula de
. La fórmula de 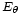 es la misma que la del caso precedente. La única diferencia es que esta vez hay de disminuir el ángulo
es la misma que la del caso precedente. La única diferencia es que esta vez hay de disminuir el ángulo 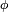 de
de 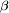 :
: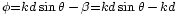
Es fácil ver que para
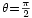 (90°) el desfase es cero.
(90°) el desfase es cero.He aquí algunos ejemplos de diagrama de radiación de una red de antenas a emisión longitudinal. Las antenas están alineadas horizontalmente. Como en el caso anterior, el diagrama solo muestra la influencia de las interferencias. Par obtener el diagrama final habría que multiplicarlos por el diagrama de radiación de cada antena individual.
Diagramas de radiación de una red de antenas isótropas a emisión longitudinal Número del diagrama Número de antenas separación entre antenas Longitud total 1 9 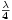
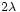
2 17 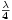
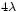
3 25 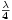
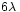
4 33 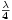
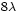
Red bidimensional de antenas
Las redes bidimensionales de antenas fueron muy utilizadas hace unas décadas para hacer emisiones direccionales en ondas cortas dirigidas horizontalmente. Esas comunicaciones servían a comunicar con otros continentes o con navíos en el mar. Por supuesto, con la utilización de comunicaciones por satélites, la comunicación comercial por ondas cortas y las enormes redes de antenas necesarias han desaparecido y no hablaremos de ellas.
Ahora otro tipo de redes de antenas es utilizado. Son las antenas utilizadas en los radares Phased arrays traducido a veces como sistema en fase. Como veremos, ese tipo de antena permite de orientar el haz del radar sin desplazar mecánicamente la antena.
Las redes bidimensionales de antenas actuales están compuestas unos miles de radiadores individuales dispuestos en una red bidimensional de malla cuadrada, rectangular o, más frecuentemente, hexagonal. Para comprender cual es el principio de funcionamiento, imagine que los emisores forman un red de malla cuadrada en la pantalla de su computadora:
 Hay un emisor en cada intersección. Si los emisores de izquierda emiten con avance de fase la emisión desvía hacia la derecha.
Hay un emisor en cada intersección. Si los emisores de izquierda emiten con avance de fase la emisión desvía hacia la derecha.si usted se sitúa lejos de la pantalla y que todos los emisores están alimentados en fase, para recibir todas la emisiones en fase, usted tendrá que ponerse en la perpendicular al plano que contiene los emisores (la pantalla) y cuyo pie está en el centro del conjunto de emisores. Si ahora cambiamos la fase de alimentación de los emisores de manera que la fase de cada emisor este en avance con respecto a su vecino de derecha (la de usted). Para recibir todas las emisiones en fase y así quedarse en el haz de la red usted tendrá que desplazarse hacia la derecha para alejarse de los emisores que emiten con avance de fase.
De la misma manera, si queremos que el haz principal vaya hacia arriba, habrá que adelantar la fase de cada emisor con respecto a sur vecino de arriba.
Una red bidimensional puede considerarse como una red lineal a emisión transversal cuyos elementos son otra red lineal a emisión transversal.
Así, supongamos que cada radiador individual tiene un diagrama de emisión de tipo
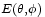 en el cual
en el cual  y
y 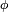 son, por ejemplo el azimut y la elevación. Una línea de emisores producirá un campo de la forma:
son, por ejemplo el azimut y la elevación. Una línea de emisores producirá un campo de la forma:Donde
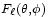 es el factor debido a la interferencia de los emisores de una línea. Ahora consideremos cada línea como un elemento de la columna. Si
es el factor debido a la interferencia de los emisores de una línea. Ahora consideremos cada línea como un elemento de la columna. Si 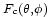 es el factor debido a la interferencia de los emisores de la columna, el diagrama de emisión total será:
es el factor debido a la interferencia de los emisores de la columna, el diagrama de emisión total será:Sin ir más lejos en los cálculos de los factores
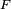 , veamos que aspecto tiene la emisión de este tipo de antena. En el caso de una red rectangular, el lóbulo principal tendrá el primer cero para un ángulo
, veamos que aspecto tiene la emisión de este tipo de antena. En el caso de una red rectangular, el lóbulo principal tendrá el primer cero para un ángulo 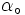 tal que:
tal que:Donde
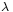 es la longitud de onda y
es la longitud de onda y 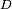 la dimensión de la red en la dirección en la cual medimos
la dimensión de la red en la dirección en la cual medimos 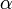 .
.Si la red es circular en lugar de ser rectangular, la fórmula precedente se convierte en:
Esta vez,
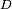 es el diámetro de la red.
es el diámetro de la red.Estas fórmulas son válidas cuando el haz es perpendicular a la red. Si el desfase hace que el haz central esté inclinado de un angulo
 con respecto a la perpendicular, el ancho (o el diámetro) eficaz de la red se encuentra reducido por un factor
con respecto a la perpendicular, el ancho (o el diámetro) eficaz de la red se encuentra reducido por un factor 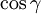 , lo que tiene como efecto de producir un lóbulo principal más ancho. Esto limita los ángulos útiles de la red bidimensional. Para cubrir correctamente la bóveda celeste hay que utilizar 3 redes con orientaciones de 120°.
, lo que tiene como efecto de producir un lóbulo principal más ancho. Esto limita los ángulos útiles de la red bidimensional. Para cubrir correctamente la bóveda celeste hay que utilizar 3 redes con orientaciones de 120°. Radar phased array de 27 m de diámetro instalado en Alaska que forma parte del " Sistema de ALerta Temprano de Misiles"
Radar phased array de 27 m de diámetro instalado en Alaska que forma parte del " Sistema de ALerta Temprano de Misiles"El interés de ese tipo de red es que con dispositivos electrónicos individuales para cada emisor (algunos miles, hemos dicho) que retardan la emisión (y la recepción) se puede cambiar la dirección en la cual "tira" el radar en microsegundos en lugar de segundos o décimos de segundos necesarios para reorientar una parábola. Eso permite al radar (militar, por supuesto) de vigilar y tratar varios blancos simultáneamente. Las aplicaciones son sobre todo militares: radares de aviones y buques de guerra y radares de sistemas anti-misiles.
Otro interés de este tipo de red, es que, como hay miles de emisores, cada uno emite algunos diezmilésimos de la potencia total de la antena. Por ejemplo, para un radar que emite con una potencia media de 500 W y que está formado por 2000 emisores individuales. Cada emisor emite solo 250 mW, lo que simplifica la electrónica.
Hay al menos una aplicación civil que utiliza este tipo de red. Se trata del sistema de comunicación por satélites Iridium. Las antenas de esos satélites concentran la emisión y recepción en una pequeña zona de la superficie de la tierra bajo el satélite y que este barrea miles de veces por segundo sobre una zona mucho mayor.
Todo eso necesita una computadora que determine el retardo a dar a cada uno de los emisores/receptores individuales y que lo transmita a cada uno de ellos. El cálculo del retardo es relativamente simple. Basta calcular la diferencia de camino recorrido entre el emisor que sirve de referencia y el emisor para el cual se hace el cálculo. Esa distancia es la proyección del segmento que une los dos emisores sobre la línea que tiene la dirección deseada de la emisión. Y para ello basta hacer el producto escalar del vector que va de un emisor al otro por el vector unitario en la dirección de la emisión
Problemas prácticos propios a la redes de antenas
En todo lo hemos expuesto precedentemente, hemos pasado por silencio la interacción entre antenas. La interacción entre elementos individuales de una red ha por efecto de inducir corrientes en los otros elementos lo cual cambia la impedancia del elemento. El resultado es que fijar la fase de la corriente de lada elemento cuando hay interacción entre ellos es muy complicado. Una manera de evitar ese problema es la de alimentar un solo elemento. De esa manera la fase de los otros elementos viene fijada únicamente por la geometría de la antena. Es el caso de las antenas Yagi-Uda. La otra manera es evitar la interacción entre antenas sea eligiendo la disposición y el tipo de radiador. Por ejemplo Los dipolos alineados tienen muy poca interacción entre ellos porque radian muy poco en la dirección de los conductores. Otra posibilidad es utilizar radiadores que no radien hacia los lados, donde se encuentran los otros radiadores. Es el caso corriente en los radares phased array.
Referencias
Electronic Radio and Engineering. F.R. Terman. MacGraw-Hill
Categoría: Antenas
Wikimedia foundation. 2010.