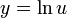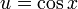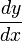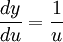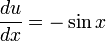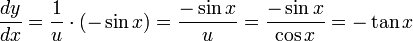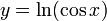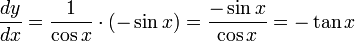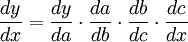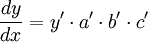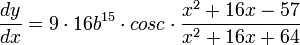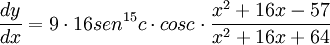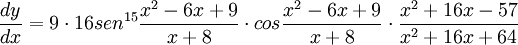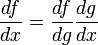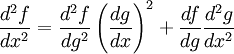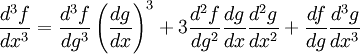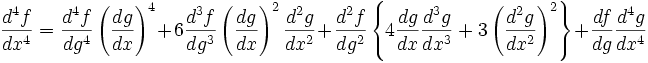- Regla de la cadena
-
Regla de la cadena
En cálculo, la regla de la cadena es una fórmula para la derivada de la composición de dos funciones. Tiene aplicaciones en el cálculo algebraico de derivadas cuando existe composición de funciones. Descripción de la regla: En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto a x puede ser computado como el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.
Contenido
Descripción algebraica
En términos algebraicos, la regla de la cadena (para funciones de una variable) afirma que si
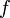 es diferenciable en
es diferenciable en 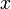 y
y 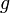 es una función diferenciable en
es una función diferenciable en 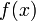 , entonces la función compuesta
, entonces la función compuesta 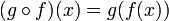 es diferenciable en
es diferenciable en 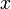 y
yNotación de Leibniz
Alternativamente, en la notación de Leibniz, la regla de la cadena puede expresarse como:
donde
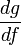 indica que g depende de f como si ésta fuera una variable.
indica que g depende de f como si ésta fuera una variable.Ejemplos de aplicación
Ejemplo conceptual
Supóngase que se está escalando una montaña a una razón de 0,5 kilómetros por hora. La razón a la cual la temperatura decrece es 6 °F por kilómetro (la temperatura es menor a elevaciones mayores). Al multiplicar 6 °F por kilómetro y 0,5 kilómetros por hora, se obtiene 3 °F por hora, es decir, la razón de cambio de temperatura con respecto al tiempo transcurrido.
Este cálculo es una aplicación típica de la regla de la cadena.
Ejemplo algebraico
Por ejemplo si y = f(u) es una función derivable de u y si además u = g(x) es una función derivable de x entonces y = f(g(x)) es una función derivable con:
o también
Ejemplo 1
y queremos calcular:
Por un lado tenemos:
y
si:
entonces:
Si definimos como función de función:
resulta que:
con el mismo resultado.
Ejemplo 2
Tenemos
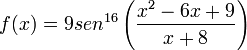 la cual se puede definir como función compuesta. Si desglosamos la función compuesta quedaría:
la cual se puede definir como función compuesta. Si desglosamos la función compuesta quedaría: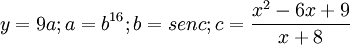 , cuyas derivadas serían:
, cuyas derivadas serían:
Con la regla de la cadena, esto sería:
Los cuales corresponden a las derivadas anteriormente extraídas.
Se reemplazan las letras b y c pos sus valores NO derivados, no confundir.
Y luego se obtiene la derivada.
Derivadas de orden superior
Las fórmulas de Faà di Bruno generalizan la regla de la cadena a derivadas de orden superior. algunas de ellas son:
Véase también
Categoría: Análisis matemático
Wikimedia foundation. 2010.

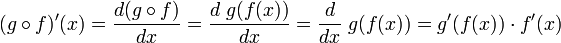
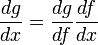
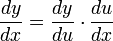
![\frac{d}{dx} [f(g(x))]=f '(g(x))\cdot g'(x)](/pictures/eswiki/56/858ff94f3748b67089b3b3a0f4048bcf.png)