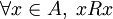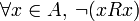Relación reflexiva

Relación reflexiva

Saltar a navegación, búsqueda

Una relación binaria R sobre un conjunto A, es reflexiva o refleja si todo elemento de A no está relacionado consigo mismo mediante R.

Es decir,

$\forall x\in A, \; xRx$

En tal caso, decimos que R cumple con la propiedad de reflexividad.

La aplicación de cualquier relación R sobre un conjunto A, se representa con el par ordenado (A, R).

Cuando una relación es lo opuesto a una reflexiva, es decir, cuando ningún elemento de A está relacionado consigo mismo mediante R, entonces decimos que es antirreflexiva, antirrefleja o irreflexiva, lo que denotamos formalmente por:

$\forall x\in A, \; \neg(xRx)$

En este caso, decimos que R cumple con la propiedad de antirreflexividad.

Representación

Sea R una relación reflexiva o antirreflexiva aplicada sobre un conjunto A, entonces R tiene una representación particular para cada forma de describir una relación binaria.

Notación	Relación reflexiva	Relación antirreflexiva
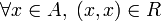
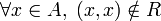
Como pares ordenados	$\forall x\in A, \; (x, x)\in R$	$\forall x\in A, \; (x, x)\notin R$
Como matriz de adyacencia	La diagonal principal de la matriz contendrá sólo 1's, es decir, 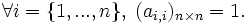$\forall i=\{1, ..., n\}, \; (a_{i,i})_{n\times n}=1.$	La diagonal principal de la matriz contendrá sólo 0's, es decir, 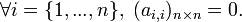$\forall i=\{1, ..., n\}, \; (a_{i,i})_{n\times n}=0.$
Como grafo	El grafo contendrá bucles en todos sus nodos.	El grafo no contendrá bucles en ninguno de sus nodos.

Ejemplos

Sea A un conjunto cualquiera:

• Sea 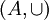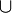$(A, \cup)$, $\cup$ es reflexiva, porque todo conjunto esta contenido en sí mismo.
• Sea 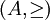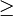$(A, \ge)$, $\ge$ ("mayor o igual que") es reflexiva, pero 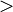$>\,$ ("mayor estricto que") no lo es.
• Sea 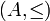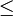$(A, \le)$, $\le$ ("menor o igual que") es reflexiva, pero 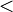$<\,$ ("menor estricto que") no lo es.
• Sea 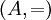$(A, =)\,$, $=\,$ (la igualdad matemática), es reflexiva.
• Sea 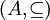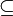$(A, \subseteq)$, $\subseteq$ (la inclusión de conjuntos), es reflexiva.
• Sea 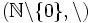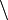$(\mathbb{N}\backslash\{0\}, \backslash)$, $\backslash\,$ (la divisibilidad) es reflexiva.
• Sea X el conjunto de todas las rectas en el plano, la relación de paralelismo || entre rectas es reflexiva, porque toda recta es paralela a sí misma.
• Sea X el conjunto de todas las rectas en el plano, la relación de perpendicularidad 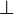$\bot$ entre dos rectas es antirreflexiva, porque no hay rectas que sean perpendiculares a sí mismas.
• Las relaciones Ser padre de y Ser madre de son antirreflexivas, porque en ningún caso alguien puede ser padre o madre de sí mismo.

Obtenido de "Relaci%C3%B3n reflexiva"