- Relación de recurrencia
-
Relación de recurrencia
Contenido
Definición
Una relación de recurrencia para una sucesión
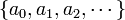 es una fórmula que expresa cada término
es una fórmula que expresa cada término 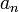 a partir de cierto
a partir de cierto 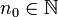 , en función de uno o más de los términos que le preceden. Los valores de los términos necesarios para empezar a calcular se llaman condiciones iniciales. Se dice que una sucesión es una solución de la relación de recurrencia si su término general verifica dicha relación.
, en función de uno o más de los términos que le preceden. Los valores de los términos necesarios para empezar a calcular se llaman condiciones iniciales. Se dice que una sucesión es una solución de la relación de recurrencia si su término general verifica dicha relación.Ejemplo
Ejemplos particulares de relaciones de recurrencia son las de las formas:
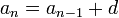 (progresión aritmética),
(progresión aritmética), 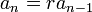 (progresión geométrica). Sus soluciones son respectivamente,
(progresión geométrica). Sus soluciones son respectivamente, 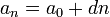 y
y 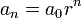 . Por otra parte uno de los ejemplos más estudiados es la sucesión de Fibonacci que viene dada por:
. Por otra parte uno de los ejemplos más estudiados es la sucesión de Fibonacci que viene dada por: 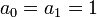 y
y 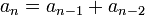 para todo
para todo 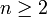
Relaciones de recurrencia lineales homogéneas
Si
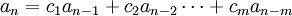 para
para 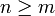 , se dice que la relación de recurrencia es lineal homogénea de orden
, se dice que la relación de recurrencia es lineal homogénea de orden 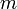 .
.Definíción
Llamaremos ecuación característica de la relación de recurrencia
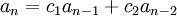 a la ecuación
a la ecuación 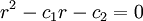 . A sus valores de solucion se les llama raices caracteristicas
. A sus valores de solucion se les llama raices caracteristicasTeorema 1
Dada la relación de recurrencia
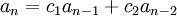 con
con 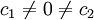 , se verifica:
, se verifica:1-
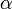 es raíz característica si y solo si
es raíz característica si y solo si 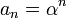 es solución de la relación de recurrencia.
2- si
es solución de la relación de recurrencia.
2- si 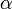 es raíz doble de la ecuación característica, entonces
es raíz doble de la ecuación característica, entonces 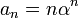 es solución de la relación de recurrencia.
3- si
es solución de la relación de recurrencia.
3- si 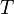 y
y 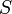 son soluciones de la relación de recurrencia, entonces
son soluciones de la relación de recurrencia, entonces 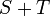 y
y 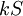 también lo son, para todo
también lo son, para todo 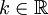
Teorema 2
Dada la relación de recurrencia
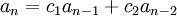 con
con 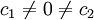 :
:1- Si la ecuación
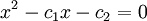 tiene dos soluciones reales distintas a
tiene dos soluciones reales distintas a 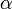 y
y 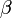 se tiene que
se tiene que 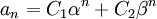 2- Si la ecuación
2- Si la ecuación 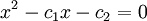 tiene una solución real doble
tiene una solución real doble 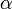 se tiene que
se tiene que 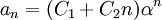 .
.
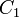 y
y 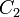 se determinan a partir de las condiciones iniciales
se determinan a partir de las condiciones iniciales 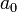 y
y 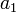 .
.
Relaciones de recurrencia lineales no homogéneas
Si
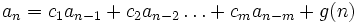 para
para 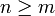 , se dice que la relación de recurencia es lineal no homogénea de orden
, se dice que la relación de recurencia es lineal no homogénea de orden 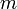 . A la relación
. A la relación 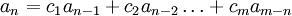 resultante de eliminar
resultante de eliminar 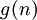 se le llama relación de recurrencia lineal homogénea asociada.
se le llama relación de recurrencia lineal homogénea asociada.Proposición
Si
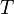 y
y 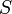 son soluciones de la relación de recurrencia lineal no homogénea, entonces
son soluciones de la relación de recurrencia lineal no homogénea, entonces 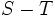 es solución de la relación de recurrencia lineal homogénea asociada.
es solución de la relación de recurrencia lineal homogénea asociada.Pasos para resolver una relación de recurrencia lineal no homogénea
- Se obtiene la solución general de la ecuación homogénea asociada. - Se obtiene una solución particular de la relación de recurrencia no homogénea. - La suma de la solución general de la ecuación lineal homogénea asociada y de una solución particular de la relación de recurrencia lineal no homogénea nos da la solución general de la relación de recurrencia lineal no homogénea. - La solución específica se obtiene a partir de las condiciones iniciales.
Observación
Una solución particular
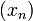 de la relación de recurrencia lineal no homogénea se puede encontrar en algunos casos especiales. - Si
de la relación de recurrencia lineal no homogénea se puede encontrar en algunos casos especiales. - Si 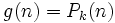 (polinomio de grado
(polinomio de grado 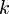 , entonces
, entonces 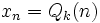 (polinomio de grado
(polinomio de grado 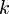 , excepto si 1 es raíz característica con multiplicidad s, en cuyo caso
, excepto si 1 es raíz característica con multiplicidad s, en cuyo caso 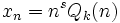 . - Si
. - Si 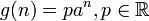 , entonces
, entonces 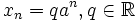 , excepto si a es raíz característica con multiplicidad s, en cuyo caso
, excepto si a es raíz característica con multiplicidad s, en cuyo caso 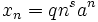 - Si
- Si 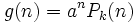 , entonces
, entonces 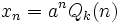 , excepto si a es raíz característica con multiplicidad s, en cuyo caso
, excepto si a es raíz característica con multiplicidad s, en cuyo caso 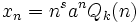 Categorías: Wikipedia:Fusionar | Relaciones | Sucesiones
Categorías: Wikipedia:Fusionar | Relaciones | Sucesiones
Wikimedia foundation. 2010.
