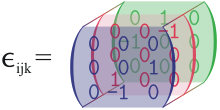
- Símbolo de Levi-Civita
-
En matemáticas, y en particular en cálculo tensorial, se define el símbolo de Levi-Civita, también llamado el símbolo de permutación, como sigue:

nombrado así por Tullio Levi-Civita. Se utiliza en muchas áreas de las matemáticas y en física. Por ejemplo, en álgebra lineal, el producto vectorial de dos vectores se puede escribir como:

o más simplemente:
esta última expresión puede ser simplificada más usando la notación de Einstein, convención en la que se puede omitir el símbolo de sumatoria. El tensor cuyas componentes son dadas por el símbolo de Levi-Civita (un tensor covariante de rango 3) a veces se llama el tensor de permutación.
El símbolo de Levi-Civita se puede generalizar a dimensiones más altas:

Ver permutación par o grupo simétrico para una definición de 'permutación par' y de 'permutación impar'.
Bibliografía
R. Byron Bird; Warren E. Stewart; Edwin N. Lightfoot (2006). «Apéndice A» (en Español). Fenómenos de Transporte (2ᵃ edición). México: Limusa Wiley. pp. 951,952. ISBN 968-18-6365-8.
Categorías:- Permutaciones
- Álgebra multilineal
Wikimedia foundation. 2010.