- Bimomento
-
Bimomento
El bimomento es un tipo de esfuerzo interno resultante de las tensiones perpendiculares (normales) a la sección transversal asociadas al alabeo seccional de un prisma mecánico. El bimomento es muy importante en situaciones de torsión alabeada requiere la aparición de un alabeo seccional considerable para ser apreciable.
Contenido
Relación con las tensiones
El bimomento resultante sobre una sección puede calcularse como integral del producto del alabeo unitario y la tensión perpendicular a una sección:
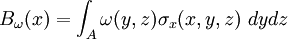
Relación con los desplazamientos
El bimomento puede considerarse un esfuerzo interno generalizado conjugado del alabeo φ (función de alabeo). Para comprobar eso puede basta examinar la expresión de la energía de deformación para un prisma mecánico sometido a flexo-torsión:
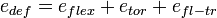
Donde cada uno de los términos anteriores se expresa en términos de los desplazamientos generalizados del eje baricéntrico y las derivadas de estos desplazamientos. Es inmediato comporbar que:
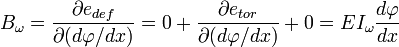
Donde se ha usado que sólo el término de energía desacoplado de torsión viene dado por:
Cálculo del bimomento
El bimomento puede ser calculado a partir de las solicitaciones por unidad de longitud, a partir del sistema de ecuaciones diferenciales:
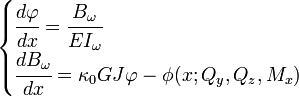
Donde:
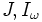 , son respectivamente el módulo de torsión, el módulo de alabeo
, son respectivamente el módulo de torsión, el módulo de alabeo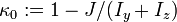 , se calcula a partir del módulo de torsión y el momento de inercia polar o suma de momentos de inercia principales.
, se calcula a partir del módulo de torsión y el momento de inercia polar o suma de momentos de inercia principales.
Derivando la segunda de estas ecuaciones y substituyendo en ella la primera relación se llega a una ecuación de segundo orden para el bimomento:
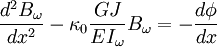
Donde la función
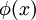 que aparece en el sistema anterior viene dada por:
que aparece en el sistema anterior viene dada por: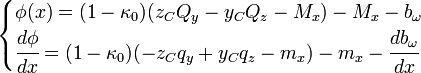
Donde (yC, zC) son las coordenadas del centro de cortante y qy, qz, mx y bω son esfuerzos por unidad de longitud que se pueden expresar a partir de la integral sobre el perímetro de la sección de las cargas superficiales que actúan sobre el prisma mecánico:
![\begin{cases}
q_y(x)= \int_P f_y(x,\bar{s}) d\bar{s} & \qquad m_x(x)=\int_P [-(z-z_C)f_y + (y-y_C)f_z]d\bar{s}\\
q_z(x)= \int_P f_z(x,\bar{s}) d\bar{s} & \qquad b_\omega(x) = \int_P \omega f_x(x,\bar{s}) d\bar{s} \end{cases}](/pictures/eswiki/55/7600c5fe5dc16d944c045d1bbfe07d55.png)
Si no hay fuerzas de superficie en la dirección del eje baricéntrico (fx = 0) ni momentos torsores distribuidos y además el centro de cortante coincide con el baricentro, tal como sucede en un buen número de casos prácticos entonces
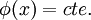 y la ecuación diferencial para el bimomento resulta ser una ecuación diferencial homogénea de muy sencilla resolución.
y la ecuación diferencial para el bimomento resulta ser una ecuación diferencial homogénea de muy sencilla resolución.Véase también
- Alabeo seccional
- Módulo de torsión, Momento de alabeo
Categoría: Resistencia de materiales
Wikimedia foundation. 2010.

![e_{tor} = \frac{1}{2} \left [
GJ \left( \frac{d\theta_x}{dx} \right)^2 +
\frac{\kappa}{1-\kappa} GJ \left( \frac{d\theta_x}{dx} - \varphi \right)^2 +
EI_\omega \left( \frac{d\varphi}{dx} \right)^2 \right]](/pictures/eswiki/49/13ddc8131d7508b4388f846570444671.png)