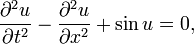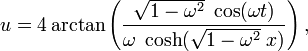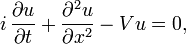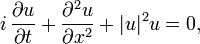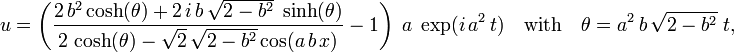- Breather
-
Breather
Un breather (habitualmente sin traducción) es una solución a un determinado sistema no lineal (bien a un sistema con muchos grados de libertad, o bien a un sistema continuo), consistente en una onda que concentra su energía de manera localizada y oscilatoria, en contraposición a la ergodicidad esperada. Los breathers aparecen como soluciones en ecuaciones de medios continuos o en redes discretas no lineales. Ejemplos del primer caso son la ecuación de sine-Gordon y la ecuación no lineal de Schrödinger. Una condición necesaria para la existencia en el segundo caso (redes discretas no lineales), es que la frecuencia principal del breather y sus armónicos se encuentren fuera del espectro de frecuencias de los fonones de la red.
Los breathers pueden ser estáticos (oscilones) o no.
El breather como solución a la ecuación de sine-Gordon
La ecuación de sine-Gordon es la ecuación en derivadas parciales:
donde u es una función de x y t: u = u(x,t)
Utilizando el método IST (Inverse Spectral Transform o Inverse Scattering Transform) se alcanza la solución:
que para ω < 1 corresponde a un breather.
El breather como solución a la ecuación no lineal de Schrödinger
En paralelismo a la ecuación de Schrödinger en una dimensión:
La ecuación no lineal de Schrödinger es la ecuación en derivadas parciales:
donde u es una función de x y t: u = u(x,t)
Por ejemplo, la solución:
para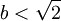 , corresponde a breathers periódicos en x.
, corresponde a breathers periódicos en x.Véase también
Categoría: Física matemática
Wikimedia foundation. 2010.