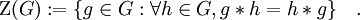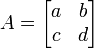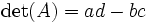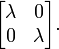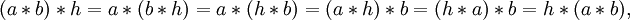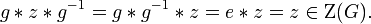- Centro de un grupo
-
Centro de un grupo
En teoría de grupos, el centro de un grupo es el conjunto (que resulta ser un subgrupo) de elementos del grupo que conmutan con todos los elementos del grupo. De manera formal, dado un grupo (G, * ), definimos el centro del grupo G como sigue:
Por ejemplo sea G el grupo gl(2, R) de las matrices 2 × 2 invertibles
con coeficientes reales. Invertibilidad equivale a que el determinante
sea diferente de 0. Entonces un cálculo directo muestra que el centro de G consiste de las matrices escalares
Este es un caso particular, del resultado a continuación:
Proposición El centro del grupo gl(n, R) de las matrices n × n invertibles consiste de las matrices diagonales constantes, es decir, aquellas que son un múltiplo de la matriz identidad.
Para otro ejemplo, sea G el grupo de los cuaterniones. Es fácil verificar que el centro de ese grupo es < − 1 > = − 1,1 pues son los únicos elementos que pueden conmutar con el resto.
Propiedades
Si G es abeliano (conmutativo) entonces G=Z(G).
Proposición. El centro Z(G) de un grupo G es un subgrupo normal abeliano de G.
Z(G) es un grupo: El elemento neutro e del grupo conmuta con todos los elementos de G y luego e ∈ Z{G). Si a, b ∈ Z(G), h ∈ G entonces
es decir que a*b ∈ Z(G). Z(G) es invariante por la operación de tomar inversas. Si a ∈ Z(G) y g ∈ G entonces a * g = g * a. Luego multiplicando por a-1 la derecha y por la izquierda tenemos que a-1 * g = g * a-1 para todo g ∈ G. Luego a-1 ∈ Z(G).
Z(G) es abeliano, pues todos sus elementos conmutan entre sí.
Z(G) es un subgrupo normal de G pues si z ∈ Z(G), entonces
Categoría: Teoría de grupos
Wikimedia foundation. 2010.