- Partícula libre
-
Partícula libre
En física, una partícula libre es una partícula que, en cierto sentido, no está enlazada. En física clásica esto significa que la partícula no está sometida a ninguna fuerza externa.
Contenido
Partícula libre clásica
La partícula libre clásica se caracteriza simplemente porque su velocidad es constante. El momento lineal viene dado por
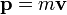
y la energía por
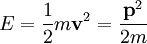
donde
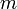 es la masa de la partícula y
es la masa de la partícula y 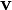 el vector velocidad de la partícula.
el vector velocidad de la partícula.Partícula libre cuántica no-relativista
La ecuación de Schrödinger dependiente del tiempo para una partícula libre es:
(1)
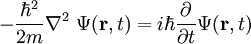
Es fácil comprobar que para este sistema el operador Hamiltoniano conmuta con el operador momento y, por tanto, existe un conjunto completo de soluciones comunes. La solución correspondiente a valores definidos de la energía y del momento viene dada por una onda plana:
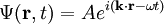
y, por tanto, con la restricción
(2)
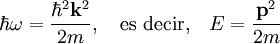
donde r es el vector posición, t es el tiempo, k es el vector de onda, ω es la frecuencia angular y A la amplitud. Una onda plana representa el estado de una partícula libre con una probabilidad uniforme en todo el espacio, debido a que la densidad de probabilidad toma un valor constante e independiente de la posición r y del tiempo t,
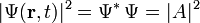 . Como la integral de
. Como la integral de 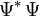 sobre todo el espacio debe de ser la unidad, hay un problema a la hora de normalizar esta autofunción del momento (una alternativa es considerar la normalización en función del flujo). Sin embargo, no será un problema para una partícula libre más general, ya que de alguna manera se encontrará localizada tanto en su posición como en su momento (véase partícula en una caja para una discusión más detallada).
sobre todo el espacio debe de ser la unidad, hay un problema a la hora de normalizar esta autofunción del momento (una alternativa es considerar la normalización en función del flujo). Sin embargo, no será un problema para una partícula libre más general, ya que de alguna manera se encontrará localizada tanto en su posición como en su momento (véase partícula en una caja para una discusión más detallada).Paquete de onda
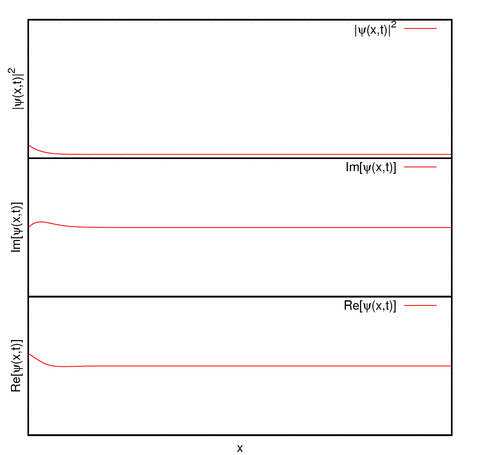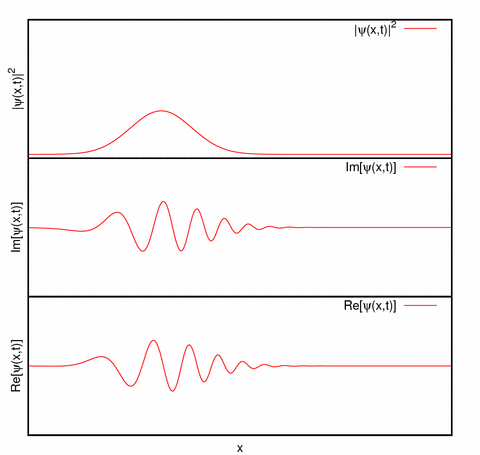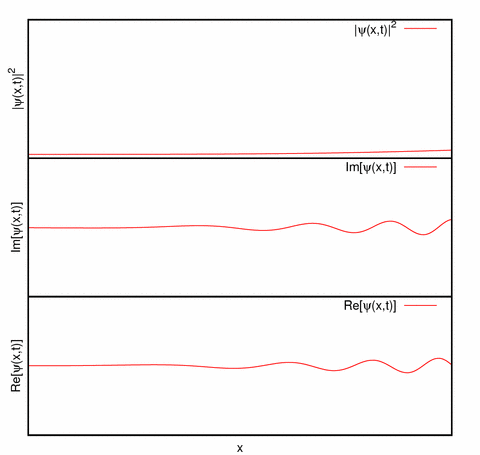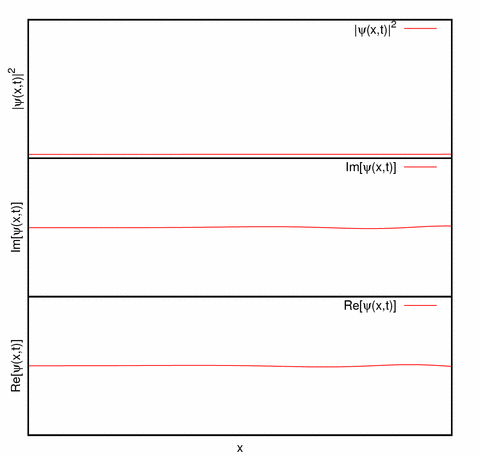 Representación de un paquete de ondas unidimensional: La parte real, parte imaginaria y la densidad de probabilidad de un paquete de ondas desplazándose hacia la derecha.
Representación de un paquete de ondas unidimensional: La parte real, parte imaginaria y la densidad de probabilidad de un paquete de ondas desplazándose hacia la derecha.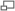
Una partícula libre más general no tiene un momento o una energía definida. En este caso, la función de onda de la partícula libre se representa como una superposición de ondas planas (que describen el estado de una partícula libre de momento definido), denominada paquete de ondas:
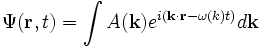
donde la integral se define sobre todo el espacio k, y donde ω depende de k según la ecuación (). Nótese que esta función, al contrario que las ondas planas, es de cuadrado integrable y, por tanto, se puede normalizar.[1]
La velocidad de grupo de la onda se define como
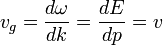
donde v es la velocidad clásica de la partícula. La velocidad de fase de la onda se define como
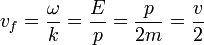
Si suponemos por simplicidad que la variación de la amplitud
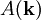 es simétrica respecto de su valor máximo
es simétrica respecto de su valor máximo 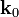 , obtenemos que el valor esperado del momento p es
, obtenemos que el valor esperado del momento p es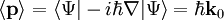
mientras que el valor esperado de la energía E es
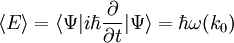
Despejando
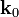 y ω y sustituyendo en la ecuación que las relaciona, obtenemos la relación ya conocida entre energía y momento para partículas no-relativistas con masa m
y ω y sustituyendo en la ecuación que las relaciona, obtenemos la relación ya conocida entre energía y momento para partículas no-relativistas con masa m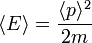
donde p=|p|.
Densidad de corriente en mecánica cuántica
En mecánica cuántica, la corriente de probabilidad es un concepto que describe el flujo de densidad de probabilidad. Así, en mecánica cuántica no-relativista, se define como
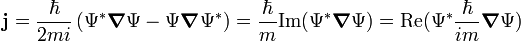
Para el caso de una partícula libre
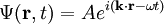 , la corriente de probabilidad viene dada por
, la corriente de probabilidad viene dada por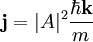
Partícula libre relativista
Hay varias ecuaciones que describen las partículas relativistas. Para una descripción de las soluciones para una partícula libre ver los artículos:
- La ecuación de Klein-Gordon describe partículas cuánticas relativistas sin carga ni espín
- La ecuación de Dirac describe el electrón relativista (cargado, espín 1/2)
Referencias
- ↑ En efecto, la función de onda representa la transformada de Fourier de la amplitud. Así, normalmente se define como
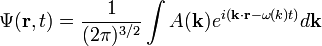
que, de acuerdo con la relación de Parseval es una función de cuadrado integrable siempre que lo sea la amplitud
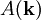 .
.
.
- Claude Cohen-Tannoudji; Bernard Diu et Frank Laloë (1977). Mécanique quantique, vol. I et II. Paris: Collection Enseignement des sciences (Hermann). ISBN 2-7056-5767-3.
Categorías: Conceptos fundamentales de la física | Mecánica clásica | Mecánica cuántica
Wikimedia foundation. 2010.
