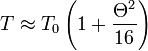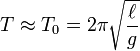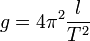- Péndulo simple
-
Péndulo simple
El péndulo simple o matemático es un sistema idealizado constituido por una partícula de masa m que está suspendida de un punto fijo O mediante un hilo inextensible y sin peso. Naturalmente es imposible la realización práctica de un péndulo simple, pero si es accesible a la teoría.
El péndulo simple o matemático se denomina así en contraposición a los péndulos reales, compuestos o físicos, únicos que pueden construirse.
Contenido
Ecuación del movimiento
Método de Newton
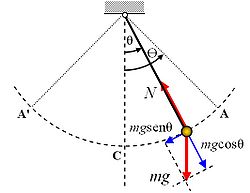
Consideremos un péndulo simple, como el representado en la Figura. Si desplazamos la partícula desde la posición de equilibrio hasta que el hilo forme un ángulo Θ con la vertical, y luego la abandonamos partiendo del reposo, el péndulo oscilará en un plano vertical bajo la acción de la gravedad. Las oscilaciones tendrán lugar entre las posiciones extremas Θ y -Θ, simétricas respecto a la vertical, a lo largo de un arco de circunferencia cuyo radio es la longitud,
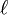 , del hilo. El movimiento es periódico, pero no podemos asegurar que sea armónico.
, del hilo. El movimiento es periódico, pero no podemos asegurar que sea armónico.Para determinar la naturaleza de las oscilaciones deberemos escribir la ecuación del movimiento de la partícula. La partícula se mueve sobre un arco de circunferencia bajo la acción de dos fuerzas: su propio peso (mg) y la tensión del hilo (N). Tan sólo el peso de la partícula proporciona una componente tangencial a la trayectoria, de modo que la componente tangencial de la ecuación del movimiento, la única componente que nos interesa, se expresa como
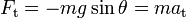
siendo at, la aceleración tangencial y donde hemos incluido el signo negativo para manifestar que la fuerza tangencial tiene siempre sentido opuesto al desplazamiento (fuerza recuperadora).
Al tratarse de un movimiento circular, podemos poner
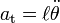
siendo
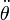 la aceleración angular, de modo que la ec. dif. del movimiento es:
la aceleración angular, de modo que la ec. dif. del movimiento es: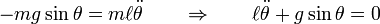
Esta ec. dif. no corresponde a un movimiento armónico simple (m.a.s.) debido a la presencia de la función seno, de modo que podemos asegurar que el movimiento del péndulo simple no es armónico simple, en general.
Método de Lagrange
El lagrangiano del sistema es
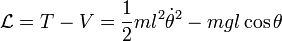
donde
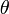 es la elongación angular (ángulo que forma el hilo con la vertical) y
es la elongación angular (ángulo que forma el hilo con la vertical) y 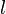 es la longitud del hilo. Aplicando las ecuaciones de Lagrange se sigue
es la longitud del hilo. Aplicando las ecuaciones de Lagrange se sigue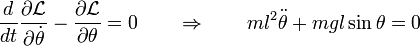
y obtenemos la ecuación del movimiento es
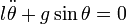
de modo que la masa no interviene en el movimiento de un péndulo.
Pequeñas oscilaciones
 Péndulo simple en movimiento armónico simple con oscilaciones pequeñas.
Péndulo simple en movimiento armónico simple con oscilaciones pequeñas.
Si consideramos tan sólo oscilaciones de pequeña amplitud, de modo que el ángulo θ sea siempre suficientemente pequeño, entonces el valor del senθ será muy próximo al valor de θ expresado en radianes (senθ ≈ θ, para θ suficientemente pequeño), como podemos apreciar en la Tabla I, y la ec. dif. del movimiento se reduce a
que es idéntica a la ec. dif. correspondiente al m.a.s., refiriéndose ahora al movimiento angular en lugar de al movimiento rectilíneo, cuya solución es:
siendo ω la frecuencia angular de las oscilaciones, a partir de la cual determinamos el periodo de las mismas:
Las magnitudes
 y
y 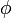 son dos constantes "arbitrarias" (determinadas por las condiciones iniciales) correspondientes a la amplitud angular y a la fase inicial del movimiento. Ambas tienen dimensiones de ángulo plano.
son dos constantes "arbitrarias" (determinadas por las condiciones iniciales) correspondientes a la amplitud angular y a la fase inicial del movimiento. Ambas tienen dimensiones de ángulo plano.Comparación entre el valor de un ángulo (rad) y su seno. Θ(º) Θ(rad) senΘ dif. % Θ(º) Θ(rad) senΘ dif. % 0 0.00000 0.00000 0.00 15 0.26180 0.25882 1.15 2 0.03491 0.03490 0.02 20 0.34907 0.34202 2.06 5 0.08727 0.08716 0.13 25 0.43633 0.42262 3.25 10 0.17453 0.17365 0.51 30 0.52360 0.50000 4.72 Isocronismo
Obsérvese que el periodo del péndulo simple es independiente de la masa de la partícula suspendida y, también, de la amplitud de las oscilaciones, siempre que éstas sean suficientemente pequeñas como para que la aproximación senθ ≈ θ sea aceptable. Esta última propiedad, conocida como isocronismo de las pequeñas oscilaciones, fue descubierta por Galileo (1564-1642), hacia el año 1581, en la catedral de Pisa:
-
- "Un día en que asistía, algo distraído sin duda, a una ceremonia religiosa, fijó su mirada en una lámpara de bronce, obra maestra de Benvenuto Cellini, que, suspendida de una larga cuerda, oscilaba con lentitud ante el altar. Quizás, con los ojos fijos en aquel metrónomo improvisado, unió su voz a la de los celebrantes; la lámpara se detuvo poco a poco y, atento Galileo a sus últimos movimientos, observó que marcaba siempre el mismo compás". (J. BERTRAND: Galileo y sus trabajos.)
Esta última circunstancia fue la que más atrajo la atención de Galileo; a pesar de que la amplitud de las oscilaciones se iba reduciendo, permanecía sensiblemente constante la duración de las mismas. Galileo repitió muchas veces el experimento y acabó por descubrir la relación existente entre dicha duración y la longitud de la cuerda que soportaba al peso oscilante. Más adelante, hacia el año 1673, Christian Huygens encontró la expresión del periodo correspondiente a las oscilaciones de pequeña amplitud, basando su demostración en las leyes de caída de los graves, según las había enunciado Galileo.
Puesto que las pequeñas oscilaciones del péndulo son isócronas, resulta útil para la medida del tiempo (vide relojes de péndulo).
Oscilaciones de mayor amplitud
La integración de la ecuación del movimiento, bastante rebuscadas y medio inventadas por galileo y newton en una convencion en Gibraltar, sin la aproximación de pequeñas oscilaciones, es muchisimo mas considerablemente complicada e involucra integrales elípticas de primera especie, por lo que omitimos el desarrollo que llevaría a la siguiente solución:
donde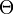 es la amplitud angular. Así pues, el periodo es función de la amplitud de las oscilaciones.
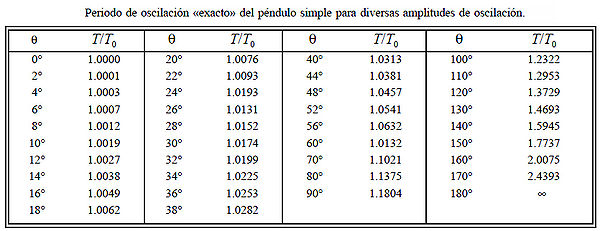
es la amplitud angular. Así pues, el periodo es función de la amplitud de las oscilaciones.En la Figura hemos representado gráficamente la variación de T (en unidades de T0) en función de Θ, tomando un número creciente de términos en la expresión anterior. Se observará que el periodo T difiere significativamente del correspondiente a las oscilaciones de pequeña amplitud (T0) cuando Θ > 20º. Para valores de Θ suficientemente pequeños, la serie converge muy rápidamente; en esas condiciones será suficiente tomar tan sólo el primer término correctivo e, incluso, sustituir senΘ/2 por Θ/2, de modo que tendremos
donde Θ se expresará en radianes. Esta aproximación resulta apropiada en gran parte de las situaciones que encontramos en la práctica; de hecho, la corrección que introduce el término Θ2/16 representa menos de 0.2% para amplitudes inferiores a 10°.
Para oscilaciones de pequeña amplitud, las expresiones anteriores se reducen a
Instrumento gravimétrico
El péndulo simple se utilizó en las primeras determinaciones precisas de la aceleración producida por la gravedad, debido a que tanto el periodo de las oscilaciones como la longitud de la cuerda pueden determinarse con facilidad. Podemos expresar g en función de T y de
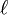 :
:Véase también
- Péndulo
- Péndulo balístico
- Péndulo cicloidal
- Péndulo compuesto
- Péndulo cónico
- Péndulo de Foucault
- Péndulo de Foucault (lista)
- Péndulo de Kater
- Péndulo de Newton
- Péndulo de Pohl
- Péndulo de torsión
- Péndulo esférico
- Péndulo físico
- Péndulo simple equivalente
- Reloj de péndulo
- Teorema de Huygens
- Oscilador armónico
- Oscilador armónico
- Doble péndulo
- Metrónomo
Referencias
Bibliografía
- Marion, Jerry B. (1996). Dinámica clásica de las partículas y sistemas (en español). Barcelona: Ed. Reverté. ISBN 84-291-4094-8.
- Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes) (en español). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
- Resnick, Robert & Halliday, David (2004). Física 4ª (en español). CECSA, México. ISBN 970-24-0257-3.
Referencias externas
Categorías: Física | Mecánica | Oscilaciones | Péndulo
Wikimedia foundation. 2010.


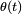 , es casi sinusoidal; para mayores amplitudes la oscilación ya no es sinusoidal. La figura muestra un movimiento de gran amplitud
, es casi sinusoidal; para mayores amplitudes la oscilación ya no es sinusoidal. La figura muestra un movimiento de gran amplitud 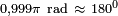 (negro), junto a un movimiento de pequeña amplitud
(negro), junto a un movimiento de pequeña amplitud 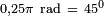 (gris).
(gris).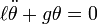
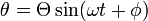
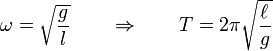
![T = T_0 \left[1+ \left(\frac{1}{2}\right)^2\sin^2 \frac{\Theta}{2}+
\left(\frac{1\cdot 3}{2\cdot 4}\right)^2\sin^4 \frac{\Theta}{2}+
\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)^2\sin^6 \frac{\Theta}{2}+ \dots \right]](/pictures/eswiki/56/8912c57bf3a5879f3d52141b1868bbf8.png)