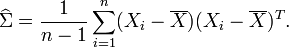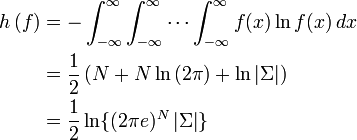- Distribución normal multivariante
-
Distribución normal multivariante
Normal multivariante Función de distribución de probabilidad Parámetros ![\mu = [\mu_1, \dots, \mu_n]^T](/pictures/eswiki/53/512027eb03498597a1106c5c3326e7a5.png) (vector real)
(vector real)
Σ matriz de covarianza (matriz real definida positiva de dimensión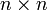 )
)Dominio 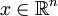
Función de densidad (pdf) 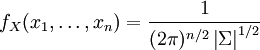
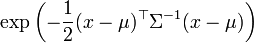
Función de distribución (cdf) Sin expresión analítica Media 
Mediana 
Moda 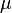
Varianza 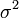
Coeficiente de simetría 0 Curtosis 0 Entropía 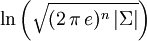
Función generadora de momentos (mgf) 
Función característica 
En probabilidad y estadística, una distribución normal multivariante, también llamada distribución gaussiana multivariante, es una generalización de la distribución normal unidimensional a dimensiones superiores.
Caso general
Un vector aleatorio
![\ X = [X_1, \dots, X_n]^T](/pictures/eswiki/51/3486ba805ca348ac5cedb6c7467cffc2.png) sigue una distribución normal multivariante si satisface las siguientes condiciones equivalentes:
sigue una distribución normal multivariante si satisface las siguientes condiciones equivalentes:- Toda combinación lineal
 está normalmente distribuida.
está normalmente distribuida. - Hay un vector aleatorio
![\ Z = [Z_1, \dots, Z_M]^T](/pictures/eswiki/56/8fb0ab0c4da8717c6b5cb36bc5d60b6d.png) , cuyas componentes son independientes son variables aleatorias distribuidas según la normal estándar, un vector
, cuyas componentes son independientes son variables aleatorias distribuidas según la normal estándar, un vector ![\ \mu = [\mu_1, \dots, \mu_n]^T](/pictures/eswiki/51/312fbb657d0f427a90a89e78fc20a418.png) y una matriz
y una matriz 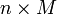
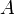 tal que
tal que 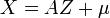 .
. - Hay un vector μ y una matriz semidefinida positiva simétrica
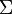 tal que la función característica de X es
tal que la función característica de X es
Si
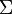 es una matriz no singular, entonces la distribución puede describirse por la siguiente función de densidad:
es una matriz no singular, entonces la distribución puede describirse por la siguiente función de densidad:donde
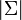 es el determinante de
es el determinante de 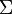 . Nótese como la ecuación de arriba se reduce a la distribución normal si
. Nótese como la ecuación de arriba se reduce a la distribución normal si 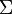 es un escalar (es decir, una matriz 1x1).
es un escalar (es decir, una matriz 1x1).El vector μ en estas circunstancias es la esperanza de X y la matriz
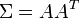 es la matriz de covarianza de las componentes Xi.
es la matriz de covarianza de las componentes Xi.Es importante comprender que la matriz de covarianza debe ser singular (aunque no esté así descrita por la fórmula de arriba, para la cual
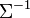 está definida).
está definida).Este caso aparece con frecuencia en estadística; por ejemplo, en la distribución del vector de residuos en problemas ordinarios de regresión lineal. Nótese también que los Xi son en general no independientes; pueden verse como el resultado de aplicar la transformación lineal A a una colección de variables normales Z.
Esta distribución de un vector aleatorio X que sigue una distribución normal multivariante puede ser descrita con la siguiente notación:
o hacer explícito que X es n-dimensional,
Función de distribución
La función de distribución F(x) se define como la probabilidad de que todos los valores de un vector aleatorio X sean menores o iguales que los valores correspondientes de un vector x. Aunque F no tenga una fórmula, hay una serie de algoritmos que permiten estimarla numéricamente.[1]
Un contraejemplo
El hecho de que dos variables aleatorias X e Y sigan una distribución normal, cada una, no implica que el par (X, Y) siga una distribución normal conjunta. Un ejemplo simple se da cuando Y = X si |X| > 1 e Y = −X si |X| < 1. Esto también es cierto para más de dos variables aleatorias.[2]
Normalmente distribuidas e independencia
Si X e Y están normalmente distribuidas y son independientes, su distribución conjunta también está normalmente distribuida, es decir, el par (X, Y) debe tener una distribución normal bivariante. En cualquier caso, un par de variables aleatorias normalmente distribuidas no tienen por qué ser independientes al ser consideradas de forma conjunta.
Caso bivariante
En el caso particular de dos dimensiones, la función de densidad (con media (0, 0) es
donde ρ es el coeficiente de correlacion entre X e Y. En este caso,
Transformación afín
Si
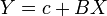 es una transformación afín de
es una transformación afín de 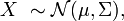 donde
donde  es un
es un 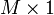 vector de constantes y
vector de constantes y 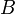 una
una 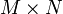 matriz, entonces
matriz, entonces 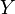 tiene una distribución normal multivariante con esperanza
tiene una distribución normal multivariante con esperanza 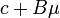 y varianza
y varianza 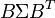 esto es,
esto es, 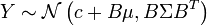 . En particular, cualquier subconjunto de las
. En particular, cualquier subconjunto de las  tiene una distribución marginal que es también una normal multivariante.
tiene una distribución marginal que es también una normal multivariante.Para ver esto, considérese el siguiente ejemplo: para extraer el subconjunto
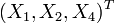 , úsese
, úseselo que extrae directamente los elementos deseados.
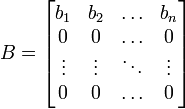
Otro corolario sería que la distribución de
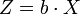 , donde b es un vector de la misma longitud que X y el punto indica un producto vectorial, sería una distribución gaussiana unidimensional con
, donde b es un vector de la misma longitud que X y el punto indica un producto vectorial, sería una distribución gaussiana unidimensional con 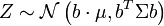 . Este resultado se obtiene usando
. Este resultado se obtiene usandoy considerando sólo la primera componente del producto (la primera fila de B es el vector b). Obsérvese cómo la definición positiva de Σ implica que la varianza del producto vectorial debería ser positiva.
Interpretación geométrica
Las curvas de equidensidad de una distribución normal multivariante son elipsoides (es decir, transformaciones lineales de hiperesferas) centrados en la mdia.[3] Las direcciones de los ejes principales de los elipsoides vienen dados por los vectores propios de la matriz de covarianza Σ. Las longitudes relativas de los cuadrados de los ejes principales vienen dados por los correspondientes vectores propios.
Si Σ = UΛUT = UΛ1 / 2(UΛ1 / 2)T es una descomposición espectral donde las columnas de U son vectores propios unitarios y Λ es una matriz diagonal de valores propios, entonces tenemos
Además, U puede elegirse de tal modo que sea una matriz de rotación, tal que invirtiendo un eje no tenga ningún efecto en N(0,Λ), pero invirtiendo una columna, cambie el signo del determinante de U'. La distribución N(μ,Σ) es en efecto N(0,I) escalada por Λ1 / 2, rotada por U y trasladada por μ.
Recíprocamente, cualquier elección de μ, matriz de rango completo U, y valores diagonales positivos Λi cede el paso a una distribución normal no singular multivariante. Si cualquier Λi es cero y U es cuadrada, la matriz de covarianza UΛUT es una singular. Geométricamente esto significa que cada curva elipsoide es infinitamente delgada y tiene volumen cero en un espacio n-dimensional, así como, al menos, uno de los principales ejes tiene longitud cero.
Correlaciones e independencia
En general, las variables aleatorias pueden ser incorreladas, pero altamente dependientes. Pero si un vector aleatorio tiene una distribución normal multivariante, entonces cualesquiera dos o más de sus componentes que sean incorreladas, son independientes.
Pero no es cierto que dos variables aleatorias que están (separadamente, marginalmente) normalmente distribuidas e incorreladas sean independientes. Dos variables aleatorias que están normalmente distribuidas pueden que no lo estén conjuntamente. Para un ejemplo de dos variables normalmente distribuidas que sean incorreladas pero no independientes, véase normalmente distribuidas e incorreladas no implica independencia.
Momentos más altos
El momento de k-ésimo orden de X se define como
donde
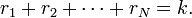
Los momentos centrales de orden k viene dados como sigue:
(a) Si k es impar,
 .
.(b) Si k es par, con k = 2λ, entonces
donde la suma se toma sobre todas las disposiciones de conjuntos
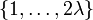 en λ parejas (no ordenadas). Esto es, si se tiene un k-ésimo ( = 2λ = 6) momento central, se estarán sumando los productos de λ = 3 covarianzas (la notación -μ se ha despreciado para facilitar la lectura):
en λ parejas (no ordenadas). Esto es, si se tiene un k-ésimo ( = 2λ = 6) momento central, se estarán sumando los productos de λ = 3 covarianzas (la notación -μ se ha despreciado para facilitar la lectura):Esto da lugar a (2λ − 1)! / (2λ − 1(λ − 1)!) términos en la suma (15 en el caso de arriba), cada uno siendo el producto de λ (3 en este caso) covarianzas. Para momentos de cuarto orden (cuatro variables) hay tres términos. Para momentos de sexto orden hay 3 × 5 = 15 términos, y para momentos de octavo orden hay 3 × 5 × 7 = 105 términos.
Las covarianzas son entonces determinadas mediante el reemplazo de los términos de la lista
![\left[ 1,\dots,2\lambda \right]](/pictures/eswiki/50/218c7d67059fcf04a548d845d9f6e1d7.png) por los términos correspondientes de la lista que consiste en r1 unos, entonces r2 doses, etc... Para ilustrar esto, examínese el siguiente caso de momento central de cuarto orden:
por los términos correspondientes de la lista que consiste en r1 unos, entonces r2 doses, etc... Para ilustrar esto, examínese el siguiente caso de momento central de cuarto orden:donde σij es la covarianza de Xi y Xj. La idea del método de arriba es que primero se encuentra el caso general para el momento k-ésimo, donde se tiene k diferentes variables X -
![E\left[ X_i X_j X_k X_n\right]](/pictures/eswiki/99/cf7446bc0444c0d68bd8dd68dd68a195.png) y entonces se pueden simplificar apropiadamente. Si se tiene
y entonces se pueden simplificar apropiadamente. Si se tiene ![E\left[ X_i^2 X_k X_n\right]](/pictures/eswiki/98/bdf61709456f398f3ff0535c90a2da35.png) entonces, simplemente sea Xi = Xj y se sigue que
entonces, simplemente sea Xi = Xj y se sigue que 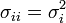 .
.Distribuciones condicionales
Si μ y Σ son divididas como sigue:
 con tamaños
con tamaños 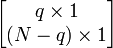
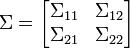 con tamaños
con tamaños 
entonces la distribución de x1 condicionada a x2 = a es una normal multivariante
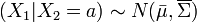 donde
dondey matriz de covarianza
Esta matriz es el complemento de Schur de
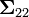 en
en 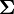 . Esto significa que para calcular la matriz condicional de covarianza, se invierte la matriz global de covarianza, se desprecian las filas y columnas correspondientes a las variables bajo las cuales está condicionada y entonces se invierte de nuevo para conseguir la matriz condicional de covarianza.
. Esto significa que para calcular la matriz condicional de covarianza, se invierte la matriz global de covarianza, se desprecian las filas y columnas correspondientes a las variables bajo las cuales está condicionada y entonces se invierte de nuevo para conseguir la matriz condicional de covarianza.Nótese que se sabe que x2 = a altera la varianza, aunque la nueva varianza no dependa del valor específico de a; quizás más sorprendentemente, la media se cambia por
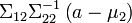 ; compárese esto con la situación en la que no se conoce el valor de a, en cuyo caso x1 tendría como distribución
; compárese esto con la situación en la que no se conoce el valor de a, en cuyo caso x1 tendría como distribución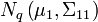 .
.La matriz
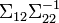 se conoce como la matriz de coeficientes de regresión.
se conoce como la matriz de coeficientes de regresión.Esperanza condicional bivariante
En el caso
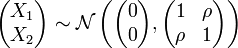
entonces
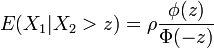
donde esta última razón se llama a menudo razón inversa de Mills.
Matriz de información de Fisher
La matriz de información de Fisher (MIF) para una distribución normal toma una formulación especial. El elemento (m,n) de la MIF para X˜N(μ(θ),Σ(θ)) es
donde
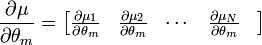
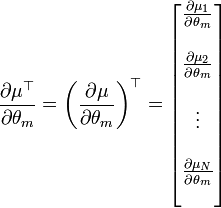
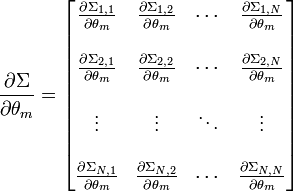
- tr is the trace function
Divergencia de Kullback-Leibler
La divergencia de Kullback-Leibler de N0N(μ0,Σ0) a N1N(μ1,Σ1) es:
El logaritmo debe tomarse con base e en los dos términos (logaritmos neperianos), siguiendo el logaritmo están los logaritmos neperianos de las expresiones que son ambos factores de la función de densidad o si no, surgen naturalmente. La divergencia de arriba se mide en nats. Dividiendo la expresión de arriba por loge 2 se da paso a la divergencia en bits.
Estimación de parámetros
La derivación del estimador de máxima verosimilitud de la matriz de covarianza de una distribución normal multivariante es, quizás sorprendentemente, sutil y elegante. Véase estimación de matrices de covarianza.
En pocas palabras, la función de densidad de probabilidad de una normal multivariante N-dimensional es
y el estimador MV de la matriz de covarianza para una muestra de n observaciones es
lo cual es, simplemente, la matriz muestral de covarianza. Este es un estimador sesgado cuya esperanza es
Una covarianza muestral insesgada es
Entropía
La entropía diferencial de la distribución normal multivariante es[4]
donde
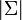 es el determinante de la matriz de covarianza Σ.
es el determinante de la matriz de covarianza Σ.Tests de normalidad multivariante
Los tests de normalidad multivariante comprueban la similitud de un conjunto dado de datos con la distribución normal multivariante. La hipótesis nula es que el conjunto de datos es similar a la distribución normal, por consiguiente un p-valor suficientemente pequeño indica datos no normales. Los tests de normalidad multivariante incluyen el test de Cox-Small[5] y la adaptación de Smith y Jain [6] del test de Friedman-Rafsky.
Dibujando valores de la distribución
Un metodo ampliamente usado para el dibujo de un vector aleatorio X de la distribución normal multivariante N-dimensional con vector de medias μ y matriz de covarianza Σ (requerida para ser simétrica y definida positiva) funciona como sigue:
- Se calcula la descomposición de Cholesky de Σ, esto es, se encuentra la única matriz triangular inferior A tal que
 . Nótese que cualquier otra matriz A que satisfaga esta condición, o sea, que es uno la raíz cuadrada de Σ, podría usarse, pero a menudo encontrar tal matriz, distinta de la de la descomposición de Cholesky, sería bastante más costoso en términos de computación.
. Nótese que cualquier otra matriz A que satisfaga esta condición, o sea, que es uno la raíz cuadrada de Σ, podría usarse, pero a menudo encontrar tal matriz, distinta de la de la descomposición de Cholesky, sería bastante más costoso en términos de computación. - Sea
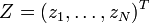 un vector cuyas componentes N normales e independientes varían (lo cual puede generarse, por ejemplo, usando la transformada de Box-Muller.
un vector cuyas componentes N normales e independientes varían (lo cual puede generarse, por ejemplo, usando la transformada de Box-Muller. - Sea
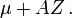
Referencias
- ↑ Véase MVNDST en [1] (incluye código FORTRAN) o [2] (incluye código MATLAB).
- ↑ Véase también normalmente distribuidas e incorreladas no implica independencia
- ↑ Nikolaus Hansen. «The CMA Evolution Strategy: A Tutorial» (PDF).
- ↑ Gokhale, DV; NA Ahmed, BC Res, NJ Piscataway (May de 1989). «Entropy Expressions and Their Estimators for Multivariate Distributions» Information Theory, IEEE Transactions on. Vol. 35. n.º 3. pp. 688–692. DOI 10.1109/18.30996.
- ↑ Cox, D. R.; N. J. H. Small (August de 1978). «Testing multivariate normality» Biometrika. Vol. 65. n.º 2. pp. 263–272. DOI 10.1093/biomet/65.2.263.
- ↑ Smith, Stephen P.; Anil K. Jain (September de 1988). «A test to determine the multivariate normality of a dataset» IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 10. n.º 5. pp. 757–761. DOI 10.1109/34.6789.
Categorías: Distribuciones continuas | Distribuciones continuas multivariantes - Toda combinación lineal
Wikimedia foundation. 2010.

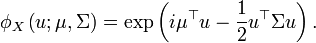
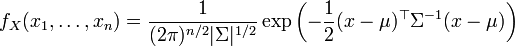
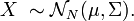
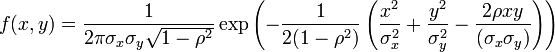
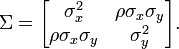
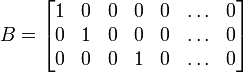
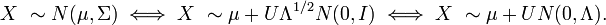
![\mu _{1,\dots,N}(X)\ \stackrel{\mathrm{def}}{=}\ \mu _{r_{1},\dots,r_{N}}(X)\ \stackrel{\mathrm{def}}{=}\ E\left[
\prod\limits_{j=1}^{N}X_j^{r_{j}}\right]](/pictures/eswiki/56/8e895d7ed390749881b8992984ae3fa8.png)
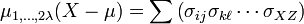
![\begin{align}
& {} E[X_1 X_2 X_3 X_4 X_5 X_6] \\
&{} = E[X_1 X_2 ]E[X_3 X_4 ]E[X_5 X_6 ] + E[X_1 X_2 ]E[X_3 X_5 ]E[X_4 X_6] + E[X_1 X_2 ]E[X_3 X_6 ]E[X_4 X_5] \\
&{} + E[X_1 X_3 ]E[X_2 X_4 ]E[X_5 X_6 ] + E[X_1 X_3 ]E[X_2 X_5 ]E[X_4 X_6 ] + E[X_1 X_3]E[X_2 X_6]E[X_4 X_5] \\
&+ E[X_1 X_4]E[X_2 X_3]E[X_5 X_6]+E[X_1 X_4]E[X_2 X_5]E[X_3 X_6]+E[X_1 X_4]E[X_2 X_6]E[X_3 X_5] \\
& + E[X_1 X_5]E[X_2 X_3]E[X_4 X_6]+E[X_1 X_5]E[X_2 X_4]E[X_3 X_6]+E[X_1 X_5]E[X_2 X_6]E[X_3 X_4] \\
& + E[X_1 X_6]E[X_2 X_3]E[X_4 X_5 ] + E[X_1 X_6]E[X_2 X_4 ]E[X_3 X_5] + E[X_1 X_6]E[X_2 X_5]E[X_3 X_4].
\end{align}](/pictures/eswiki/52/477220038abb3f6d2ee172e33bcde13f.png)
![E\left[ X_i^4\right] = 3\sigma _{ii}^2](/pictures/eswiki/55/7ee572fbf3fbe2077e2f886d7710d1d4.png)
![E\left[ X_i^3 X_j\right] = 3\sigma _{ii} \sigma _{ij}](/pictures/eswiki/98/bd7a84adc118f6fef0d3e44fd515f707.png)
![E\left[ X_i^2 X_j^2\right] = \sigma _{ii}\sigma_{jj}+2\left( \sigma _{ij}\right) ^2](/pictures/eswiki/52/4b34e16082722ca5e14bc525aa275597.png)
![E\left[ X_i^2X_jX_k\right] = \sigma _{ii}\sigma _{jk}+2\sigma _{ij}\sigma _{ik}](/pictures/eswiki/101/ea55493c283fd864bcbe46c5da9c4ee5.png)
![E\left[ X_i X_j X_k X_n\right] = \sigma _{ij}\sigma _{kn}+\sigma _{ik}\sigma _{jn}+\sigma _{in}\sigma _{jk}.](/pictures/eswiki/54/67659b5bf0652636330890c6b45712d7.png)

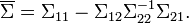
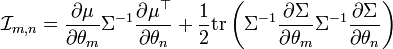
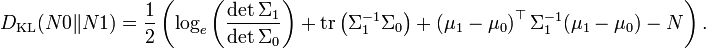

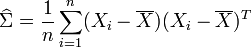
![E[\widehat\Sigma] = {n-1 \over n}\Sigma.](/pictures/eswiki/54/6f5b2fd1317b7743d57df74a3e9350dc.png)