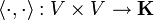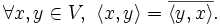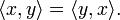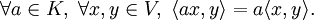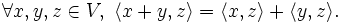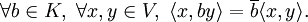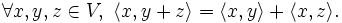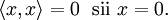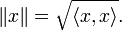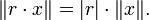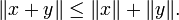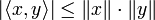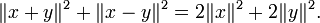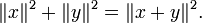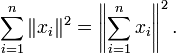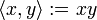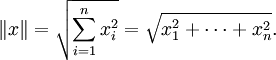- Espacio prehilbertiano
-
Espacio prehilbertiano
En matemáticas, un espacio prehilbertiano o espacio prehilbert es un espacio vectorial provisto de un producto escalar. Más concretamente, es un par
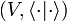 , donde
, donde 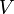 es un espacio vectorial sobre un cuerpo
es un espacio vectorial sobre un cuerpo 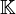 y
y 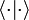 es un producto escalar en
es un producto escalar en 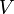 .
.El espacio prehilbertiano es un tipo de espacio métrico con la métrica inducida por la norma que como veremos puede definirse a partir del producto escalar.
Un espacio prehilbertiano que además sea un espacio completo, se dirá que es un espacio de Hilbert o hilbertiano. Si es de dimensión finita se dirá que es espacio euclídeo.
Una condición necesaria para que un espacio perhilbertiano sea un espacio de Hilbert es que el cuerpo base
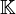 sea
sea 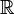 o
o 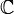 , así ningún espacio prehilbertiano sobre
, así ningún espacio prehilbertiano sobre 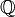 puede ser un espacio de Hilbert.
puede ser un espacio de Hilbert.Definiciones
Formalmente, un espacio prehilbertiano es un espacio vectorial V sobre un cuerpo K (Puede ser R o C), el cual posee una operación definida con la siguiente función:
llamada producto escalar, que satisface ciertos axiomas:
- Hermítica.
- Nótese que si K=R, la propiedad de hermítica es la simetría ordinaria:
- Esta condición implica que
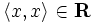 para todo
para todo 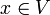 , porque
, porque 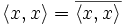 .
.
- Sesquilineal:
- Combinando esta propiedad con la de ser hermítica:
- En el caso de que el cuerpo sea R esta propiedad implica que el producto escalar es bilineal.
- Definida positiva:
-
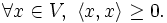 (Tiene sentido, ya que
(Tiene sentido, ya que 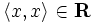 para todo
para todo 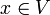 .)
.)
- Además, el único vector que al hacer el producto escalar con él mismo es cero, es el vector nulo. Esto se expresa así:
Normas en espacios prehilbertianos
En los espacios con producto escalar se define una norma
La norma está bien definida, por ser siempre el producto escalar de un vector por sí mismo un número real mayor o igual que cero. En espacios euclídeos define la "longitud" del vector x. Además se trata de una norma por cumplir las condiciones:
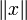 es siempre positiva y vale cero si y solamente si x vale cero.
es siempre positiva y vale cero si y solamente si x vale cero.
- Homogeneidad: para todo vector x y r un escalar:
- Desigualdad triangular: para todo vector x e y
Usando los axiomas ya mencionados podemos demostrar los siguientes teoremas:- Desigualdad de Cauchy-Schwarz: para x, y elementos en V
- la igualdad se cumple si y solo si x e y son linealmente dependientes
- Esta es una de la más importantes desigualdades en la matemática. También es conocida en la literatura matemático rusa como la desigualdad Cauchy-Bunyakowski-Schwarz
- La prueba de este teorema y sus aplicaciones pueden encontrarse en el artículo sobre la desigualdad de Cauchy-Schwarz
- Ley del paralelogramo:
- Teorema de Pitágoras: Sean x, y vectores ortogonales, entonces
- Estas últimas dos identidades sólo requieren expresar la definión de la norma en términos del producto interno, hacer las operaciones y usar los axiomas de norma.
- Una fácil generalización del teoremá pitagórico que puede ser probada por inducción es la siguiente:
- Si x1, ..., xn son vectores ortogonales, o sea, <xj, xk> = 0 para todo j, k distinto, entonces
Ejemplos
- Un ejemplo trivial son los números reales con la multiplicación estándar como producto interno.
- Más generalmente, cualquier espacio Euclideano Rn con el producto escalar es un espacio con producto interno.
- tenemos la norma:
Categoría: Análisis funcional
Wikimedia foundation. 2010.