- Conjunto parcialmente ordenado
-
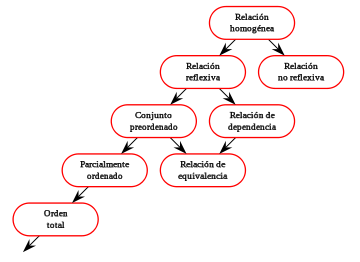
En matemáticas, especialmente en teoría del orden, un conjunto parcialmente ordenado (o poset, del inglés partially ordered set) es un conjunto equipado con una relación binaria de orden parcial. Ésta formaliza el concepto intuitivo de orden, secuencia, o arreglo de los elementos del conjunto. Un tal orden no necesariamente debe ser total, es decir, no se necesita que se puedan comparar unos con otros todos los elementos del conjunto; esto sin embargo puede ocurrir en algunos casos (en otras palabras, el orden total es un caso particular del orden parcial).
Contenido
Definición formal
Un orden parcial es una relación binaria R sobre un conjunto X que es reflexiva, antisimétrica, y transitiva, es decir, para cualesquiera a, b, y c en X se tiene que:- aRa (reflexividad).
- Si aRb y bRa, entonces a = b (antisimetría).
- Si aRb y bRc, entonces aRc (transitividad).
Un conjunto con un orden parcial se denomina conjunto parcialmente ordenado o poset. A veces se usa la expresión conjunto ordenado para uno parcialmente ordenado, siempre que quede claro que no se hará referencia a otras clases de orden. En particular, a un conjunto totalmente ordenado también se lo llama ordenado a secas, en especial en campos donde éstos son más comunes que los parcialmente ordenados.
Usualmente se usa la notación de "≤" en lugar de "R" para el orden parcial.
Ejemplos
Algunos de los ejemplos más conocidos son los siguientes:
- El conjunto de los naturales con su orden usual (la relación "menor o igual"). Este orden es además un orden total.
- El conjunto de los enteros con su orden usual. Este orden es también total.
- Un subconjunto finito {1, 2,..., n} de los naturales. Este orden es también total.
- El conjunto de naturales ordenado por la relación de divisibilidad.
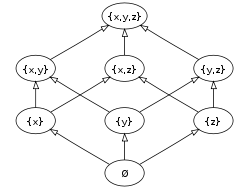
- El conjunto de subconjuntos de un conjunto dado (i.e. su conjunto de partes) ordenado por inclusión.
- El conjunto de subespacios de un espacio vectorial ordenado por inclusión.
Órdenes parciales estrictos y no estrictos
En algunos contextos, el orden parcial anteriormente definido se denomina no estricto o reflexivo; así pues, un orden parcial estricto o irreflexivo es una relación binaria que es irreflexiva y transitiva, y por lo tanto asimétrica. De forma equivalente, asimétrica (y por lo tanto irreflexiva) y transitiva.
Es decir, para cualesquiera a, b, y c en X se tiene que:
- ¬(aRa) (irreflexividad).
- Si aRb, entonces ¬(bRa) (asimetría).
- Si aRb y bRc, entonces aRc (transitividad).
Si R es un orden parcial no estricto, entonces S = R − {(a, a) | a ∈ X} es el orden parcial estricto correspondiente. Análogamente, todo orden parcial estricto S tiene uno no estricto correspondiente, a saber, S ∪ {(a, a) | a ∈ P}, o la "clausura reflexiva" de R.
Los órdenes parciales estrictos son útiles porque se corresponden más directamente con los grafos acíclicos dirigidos: todo orden parcial estricto es un G.A.D., y la clausura transitiva de un G.A.D. es, además de un orden parcial estricto, un G.A.D. en sí misma.
Número de órdenes parciales
La secuencia A001035 de la OEIS da el número de órdenes parciales en un conjunto de n elementos.
Extensión lineal
Un orden total T es una extensión lineal de un orden parcial P si, siempre que xPy, se tiene que xTy.
Esquema de temas relacionados
Teoría del orden Bien ordenado Orden total Parcialmente ordenado Preordenado Relación reflexiva Relación transitiva Relación antisimétrica Relación total Relación bien fundada Categorías:- Teoría del orden
- Conjuntos
Wikimedia foundation. 2010.