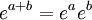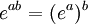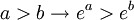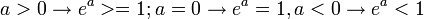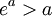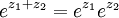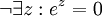- Exponenciación
-
Exponenciación
La exponenciación es una operación definible en un álgebra sobre un cuerpo normada completa o álgebra de Banach (espacio vectorial normado completo que además es un anillo) que generaliza la función exponencial de los números reales.
Contenido
Definición formal
Dado un elemento de un álgebra de Banach tenemos definidas una operación conmutativa de suma y otra de multiplicación, lo cual permite definir el anillo de polinomios sobre dicha álgebra. Además por tener una norma puede definirse para algunas series formales de potencias una noción de convergencia y por tanto de límite. En esas condiciones puede definirse la siguiente operación:
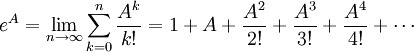
Nótese que:
- Si el cuerpo sobre la que está definida el álgebra no contiene a
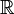 el límite anterior podría no converger, de hecho el álgebra no podría ser un álgebra de Banach.
el límite anterior podría no converger, de hecho el álgebra no podría ser un álgebra de Banach. - Si el álgebra no es un espacio vectorial normado no existe manera de establecer si el límite anterior converge.
Exponenciación de números reales
La exponenciación de números reales se realiza mediante la función exponencial. Dado un número real su exponenciación está siempre bien definida y tiene las siguientes propiedades:
Exponenciación de números complejos
La exponenciación de números complejos se define sin problemas mediante serie de potencias al igual que en el caso de números reales. Dado un número complejo separado en sus partes real e imaginaria z = a + bi su exponencación resulta ser:
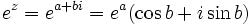
Las propiedades de la exponenciación de números complejos son similares a las de los números reales (aunque las propiedades que involucran orden no son extendibles a los complejos):
Exponenciación de números cuaterniónicos
La exponenciación de números cuaterniónicos es computacionalmente más complicada aunque está definida sin ambigüedad. Dado un cuaternión escrito en forma canónica q = a + bi + cj + dk su exponenciación resulta ser:
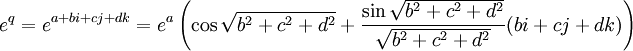
Al no ser conmutativo el producto de cuaterniones no resulta cierto que la exponenciación de una suma sea igual al producto de exponenciales de los sumandos. Por ejemplo si consideramos q1 = πi y q2 = πj tenemos:
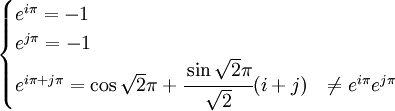
Exponenciación de matrices
Las matrices cuadrdas reales o complejas puden ser interpretadas como expresiones en una base dada de una aplicación lineal este hecho pude ser aprovechado para computar más fácilmente la exponencial de una matriz. Si A representa la matriz de una cierta aplicación lineal
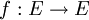 entonces la exponenciación de una matriz puede obtenerse a partir de la forma canónica de Jordan Jf de dicho endomorfismo y la matriz cambio de base C entre la base original y la base de Jordan:
entonces la exponenciación de una matriz puede obtenerse a partir de la forma canónica de Jordan Jf de dicho endomorfismo y la matriz cambio de base C entre la base original y la base de Jordan: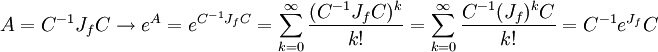
La exponencial de la forma canónica de Jordan es muy sencilla, dado un bloque de Jordan BJ, submatriz nxn, que realiza la aplicación lineal en uno de los subespacios invariantes asociados a la aplicación de Jordan se tiene que:
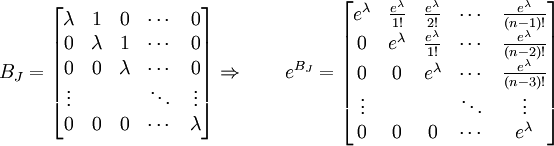
La exponenciación de matrices tiene estas otras propiedades similares a los números reales:
- Acotación de la norma:
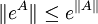
- Matriz identidad:
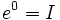
- Inverso:
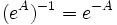
- Relación traza-determinante:
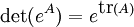
Una propiedad importante de la exponenciación de matrices es que en general, a diferencia de lo que sucede con números reales, la exponenciación de una suma de matrices no es el producto de exponenciales matrices:
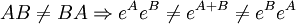
Aunque cuando el conmutador se anula sí se satisface la igualdad:
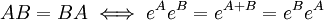
Exponenciación de operadores
La exponenciación de operadores lineales definidos sobre un espacio vectorial normado es una generalización del caso de la exponenciación de matrices. Ya que el hecho de que el espacio vectorial sea normado implica que el espacio de operadores es un espacio de Banach.
La exponenciación de operadores puede ser usada para resolver la ecuación de Schrödinger
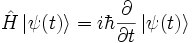
Una solución formal de esta ecuación se obtiene por exponenciación del operador hamiltoniano:
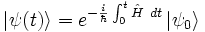
Sin embargo, en muchos casos el cálculo de la exponenciación del operador hamiltoniano puede ser computacionalmente muy complejo. Además al ser normalmente el hamiltoniano un operador no acotado la exponencial sólo podría definirse sobre un dominio del espacio de Hilbert y entonces definir una extensión del operador obtenido previamente.
Véase también
- Potenciación
- Logaritmación
Categoría: Álgebra - Si el cuerpo sobre la que está definida el álgebra no contiene a
Wikimedia foundation. 2010.