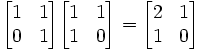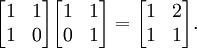- Anillo conmutativo
-
Anillo conmutativo
En teoría de anillos (una rama del álgebra abstracta), un anillo conmutativo es un anillo (R, +, ·) en el que la operación de multiplicación · es conmutativa; es decir, si para cualesquiera a, b ∈ R, a·b = b·a.
Si adicionalmente el anillo tiene un elemento unitario 1 tal que 1a = a = a1 para todo a, entonces el anillo se denomina anillo conmutativo unitario.
La rama de la teoría de anillos que estudia los anillos conmutativos se denomina álgebra conmutativa.
Ejemplos
- El ejemplo más importante es tal vez el de los números enteros con las operaciones usuales de suma y multiplicación, ambas conmutativas. Este anillo usualmente se denota por Z, por la palabra alemana Zahlen (números).
- Los números racionales, reales, y complejos forman anillos conmutativos con las operaciones usuales; más aún, son campos.
- Más generalmente, todo campo es un anillo conmutativo por definición.
- El mejor ejemplo de un anillo no conmutativo es el conjunto de matrices cuadradas de 2×2 con valores reales. Por ejemplo, la multiplicación matricial
-
- da un resultado distinto que si se invierte el orden de los factores:
- Si n > 0 es un entero, el conjunto Zn de enteros módulo n forma un anillo conmutativo con n elementos.
- Si R es un anillo conmutativo, el conjunto de polinomios de variable X con coeficientes en R forma un nuevo anillo conmutativo, denotado por R[X].
- El conjunto de números racionales de denominador impar forma un anillo conmutativo, estrictamente contenido en el anillo Q de los racionales, y que contiene propiamente al Z de los enteros.
Propiedades
- Si f : R → S es un homomorfismo de anillos entre R y S, S es conmutativo, y f es inyectiva (esto es, un monomorfismo), R también debe ser conmutativo, pues f(a·b) = f(a)·f(b) = f(b)·f(a) = f(b·a).
- Si f : R → S es un homomorfismo de anillos entre R y S, con R es conmutativo, la imagen f(R) de R será también conmutativa; en particular, si f es sobreyectiva (esto es, un epimorfismo), S será conmutativo también.
El mayor interés de los anillos conmutativos está en cuando además son unitarios, es decir, los anillos conmutativos unitarios.
Categoría: Teoría de anillos
Wikimedia foundation. 2010.