Complemento de un conjunto

El complemento de un conjunto A es otro conjunto A^∁ que contiene todos los elementos (dentro del universo U) que no están en A.

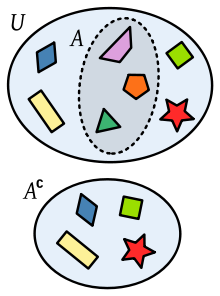
El conjunto complementario de un conjunto dado es otro conjunto que contiene todos los elementos que no están en el conjunto original. Para poder definirlo es necesario especificar qué tipo de elementos se están utilizando, o de otro modo, cuál es el conjunto universal. Por ejemplo, si se habla de números naturales, el complementario del conjunto de los números primos P es el conjunto de los números no primos C, que está formado por los números compuestos y el 1:

P = {2, 3, 5, 7, ...}

C = {1, 4, 6, 8, 9,...}

A su vez, el conjunto C es el complementario de P. El conjunto complementario se denota por una barra vertical o por el superíndice "∁", por lo que se tiene: P^∁ = C, y también C = P.

El conjunto complementario de A es la diferencia (o complementario relativo) entre el conjunto universal y A, por lo que ambas operaciones (complementario y diferencia) tienen propiedades similares.

Definición

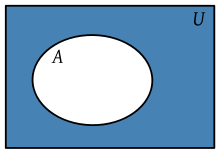Complementario de un conjunto A.

Dado un conjunto A, su complementario es el conjunto A^∁ formado por los elementos que no pertenecen a A:

El complementario de A es otro conjunto A∁ cuyos elementos son todos aquellos que no están en A: $x\in A^\complement \text{ si y s}\acute{\text{o}}\text{lo si }x\notin A$

Esta definición presupone que se ha especificado un conjunto universal U, pues de otro modo, en la afirmación "todos los x que no está en A", la palabra "todos" es ambigua. Si se menciona explícitamente el conjunto universal U, entonces el complementario de A es el conjunto de todos los elementos de U que no están en A, por lo que la relación con la diferencia es clara:

$A^\complement =U\setminus A$

Por otro lado, considerando un conjunto universal, la diferencia entre dos conjuntos puede expresarse utilizando la noción de complementariedad:

$A\setminus B=A\cap B^\complement$

Ejemplo.

• El complementario del conjunto de todos los hombres es el conjunto de todas las mujeres (hablando de personas).
• Hablando de números naturales, el complementario del conjunto {1, 5, 6, 7, 8, 10} es el conjunto {2, 3, 4, 9, 11, 12, ...}.
• El complementario del conjunto A en la imagen es la zona sombreada de azul (el conjunto universal U es toda el área del rectángulo).

Propiedades

Puesto que el conjunto universal contiene todos los elementos en consideración, y el conjunto vacío no contiene a ninguno, se tiene lo siguiente:

$U^\complement=\varnothing\text{ , }\varnothing^\complement=U$

Puesto que la noción de complementariedad está relacionada con la negación en lógica, la primera posee propiedades similares a la segunda:

Propiedad involutiva. El complementario del complementario de A es el propio A: (A∁)∁ = A La unión de un conjunto y su complementario es el conjunto universal: A ∪ A∁ = U Un conjunto y su complementario son disjuntos: A ∩ A∁ = ∅ El complementario de A está contenido en el complementario de cualquier subconjunto de A: B ⊆ A implica que A∁ ⊆ B∁

Existen también unas relaciones entre las operaciones de unión e intersección a través del complemento:

Leyes de De Morgan El complementario de la unión de dos conjuntos es la intersección de los complementarios: (A ∪ B)∁ = A∁ ∩ B∁ El complementario de la intersección de dos conjuntos es la unión de los complementarios: (A ∩ B)∁ = A∁ ∪ B∁

Véase también

• Álgebra de conjuntos
• Conjunto
• Teoría de conjuntos

Referencias

• Lipschutz, Seymour (1991). Teoría de conjuntos y temas afines. McGraw-Hill. ISBN 968-422-926-7.